CHAPTER 7
DRYING

Basic Drying Theory
Three States of Water
Heat Requirements for Vaporization
Heat Transfer in Drying
Dryer Efficiencies

Drying is one of the oldest methods of preserving food. Primitive societies practised the drying of meat and fish in the sun long before recorded history. Today the drying of foods is still important as a method of preservation. Dried foods can be stored for long periods without deterioration occurring. The principal reasons for this are that the microorganisms which cause food spoilage and decay are unable to grow and multiply in the absence of sufficient water and many of the enzymes which promote undesired changes in the chemical composition of the food cannot function without water.

Preservation is the principal reason for drying, but drying can also occur in conjunction with other processing. For example in the baking of bread, application of heat expands gases, changes the structure of the protein and starch and dries the loaf.

Drying of foods implies the removal of water from the foodstuff. In most cases, drying is accomplished by vaporizing the water that is contained in the food, and to do this the latent heat of vaporization must be supplied. There are, thus, two important process-controlling factors that enter into the unit operation of drying:

Drying processes fall into three categories:

Air and contact drying under atmospheric pressure. In air and contact drying, heat is transferred through the foodstuff either from heated air or from heated surfaces. The water vapour is removed with the air.
Vacuum drying. In vacuum drying, advantage is taken of the fact that evaporation of water occurs more readily at lower pressures than at higher ones. Heat transfer in vacuum drying is generally by conduction, sometimes by radiation.
Freeze drying. In freeze drying, the water vapour is sublimed off frozen food. The food structure is better maintained under these conditions. Suitable temperatures and pressures must be established in the dryer to ensure that sublimation occurs.

BASIC DRYING THEORY

Three States of Water

Pure water can exist in three states, solid, liquid and vapour. The state in which it is at any time depends on the temperature and pressure conditions and it is possible to illustrate this on a phase diagram, as in Fig. 7.1.

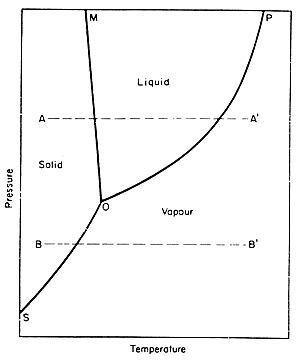
Figure 7.1 Phase diagram for water

If we choose any condition of temperature and pressure and find the corresponding point on the diagram, this point will lie, in general, in one of the three labelled regions, solid, liquid, or gas. This will give the state of the water under the chosen conditions.

Under certain conditions, two states may exist side by side, and such conditions are found only along the lines of the diagram. Under one condition, all three states may exist together; this condition arises at what is called the triple point, indicated by point O on the diagram. For water it occurs at 0.0098°C and 0.64 kPa (4.8 mm of mercury) pressure.

If heat is applied to water in any state at constant pressure, the temperature rises and the condition moves horizontally across the diagram, and as it crosses the boundaries a change of state will occur. For example, starting from condition A on the diagram adding heat warms the ice, then melts it, then warms the water and finally evaporates the water to condition A'. Starting from condition B, situated below the triple point, when heat is added, the ice warms and then sublimes without passing through any liquid state.

Liquid and vapour coexist in equilibrium only under the conditions along the line OP. This line is called the vapour pressure/temperature line. The vapour pressure is the measure of the tendency of molecules to escape as a gas from the liquid. The vapour pressure/temperature curve for water is shown in Fig. 7.2, which is just an enlargement for water of the curve OP of Fig. 7.1.

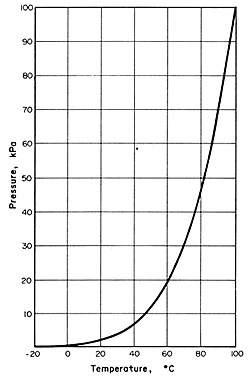
Figure 7.2. Vapour pressure/temperature curve for water

Boiling occurs when the vapour pressure of the water is equal to the total pressure on the water surface. The boiling point at atmospheric pressure is of course 100°C. At pressures above or below atmospheric, water boils at the corresponding temperatures above or below 100°C, as shown in Fig. 7.2 for temperatures below 100°C.

Heat Requirements for Vaporization

The energy, which must be supplied to vaporize the water at any temperature, depends upon this temperature. The quantity of energy required per kg of water is called the latent heat of vaporization, if it is from a liquid, or latent heat of sublimation if it is from a solid. The heat energy required to vaporize water under any given set of conditions can be calculated from the latent heats given in the steam table in Appendix 8, as steam and water vapour are the same thing.

EXAMPLE 7.1. Heat energy in air drying
A food containing 80% water is to be dried at 100°C down to moisture content of 10%. If the initial temperature of the food is 21°C, calculate the quantity of heat energy required per unit weight of the original material, for drying under atmospheric pressure. The latent heat of vaporization of water at 100°C and at standard atmospheric pressure is 2257 kJ kg^-1. The specific heat capacity of the food is 3.8 kJ kg^-1 °C^-1 and of water is 4.186 kJ kg^-1 °C^-1. Find also the energy requirement/kg water removed.

Calculating for 1 kg food
                  Initial moisture = 80%
800 g moisture are associated with 200 g dry matter.
                   Final moisture = 10 %,
100 g moisture are associated with 900 g dry matter,
Therefore (100 x 200)/900 g = 22.2 g moisture are associated with 200 g dry matter.
1kg of original matter must lose (800 - 22) g moisture = 778 g = 0.778 kg moisture.

Heat energy required for 1kg original material
                                                 = heat energy to raise temperature to 100°C + latent heat to remove water
                                                 = (100 - 21) x 3.8 + 0.778 x 2257
                                                 = 300.2 + 1755.9
                                                 = 2056 kJ.

Energy/kg water removed, as 2056 kJ are required to remove 0.778 kg of water,
                                                 = 2056/0.778
                                                 = 2643 kJ.

Steam is often used to supply heat to air or to surfaces used for drying. In condensing, steam gives up its latent heat of vaporization; in drying, the substance being dried must take up latent heat of vaporization to convert its liquid into vapour, so it might be reasoned that 1 kg of steam condensing will produce 1 kg vapour. This is not exactly true, as the steam and the food will in general be under different pressures with the food at the lower pressure. Latent heats of vaporization are slightly higher at lower pressures, as shown in Table 7.1. In practice, there are also heat losses and sensible heat changes which may require to be considered.

TABLE 7.1
LATENT HEAT AND SATURATION TEMPERATURE OF WATER

EXAMPLE 7.2. Heat energy in vacuum drying
Using the same material as in Example 7.1, if vacuum drying is to be carried out at 60°C under the corresponding saturation pressure of 20 kPa abs. (or a vacuum of 81.4 kPa), calculate the heat energy required to remove the moisture per unit weight of raw material.

Heat energy required per kg raw material
= heat energy to raise temperature to 60°C + latent heat of vaporization at 20 kPa abs.
= (60 - 21) x 3.8 + 0.778 x 2358
= 148.2 + 1834.5
= 1983 kJ.

In freeze drying the latent heat of sublimation must be supplied. Pressure has little effect on the latent heat of sublimation, which can be taken as 2838 kJ kg^-1.

EXAMPLE 7.3. Heat energy in freeze drying
If the foodstuff in the two previous examples were to be freeze dried at 0°C, how much energy would be required per kg of raw material, starting from frozen food at 0°C?

Heat energy required per kilogram of raw material= latent heat of sublimation
                               = 0.778 x 2838
                               = 2208 kJ.

Heat Transfer in Drying

We have been discussing the heat energy requirements for the drying process. The rates of drying are generally determined by the rates at which heat energy can be transferred to the water or to the ice in order to provide the latent heats, though under some circumstances the rate of mass transfer (removal of the water) can be limiting. All three of the mechanisms by which heat is transferred - conduction, radiation and convection - may enter into drying. The relative importance of the mechanisms varies from one drying process to another and very often one mode of heat transfer predominates to such an extent that it governs the overall process.

As an example, in air drying the rate of heat transfer is given by:

q = h_sA(T_a - T_s)                                                                                             (7.1)

where q is the heat transfer rate in J s^-1, h_s is the surface heat-transfer coefficient J m^-2 s^-1 °C^-1, A is the area through which heat flow is taking place, m², T_a is the air temperature and T_s is the temperature of the surface which is drying, °C.

To take another example, in a roller dryer where moist material is spread over the surface of a heated drum, heat transfer occurs by conduction from the drum to the foodstuff, so that the equation is

        q = UA(T_i– T_s )

where U is the overall heat-transfer coefficient, T_i is the drum temperature (usually very close to that of the steam), T_s is the surface temperature of the food (boiling point of water or slightly above) and A is the area of drying surface on the drum.

The value of U can be estimated from the conductivity of the drum material and of the layer of foodstuff. Values of U have been quoted as high as 1800 J m^-2 s^-1 °C^-1 under very good conditions and down to about 60 J m^-2 s^-1 °C^-1 under poor conditions.

In cases where substantial quantities of heat are transferred by radiation, it should be remembered that the surface temperature of the food may be higher than the air temperature. Estimates of surface temperature can be made using the relationships developed for radiant heat transfer although the actual effect of combined radiation and evaporative cooling is complex. Convection coefficients also can be estimated using the standard equations.

For freeze drying, energy must be transferred to the surface at which sublimation occurs. However, it must be supplied at such a rate as not to increase the temperature at the drying surface above the freezing point. In many applications of freeze drying, the heat transfer occurs mainly by conduction.

As drying proceeds, the character of the heat transfer situation changes. Dry material begins to occupy the surface layers and conduction must take place through these dry surface layers which are poor heat conductors so that heat is transferred to the drying region progressively more slowly.

Dryer Efficiencies

Energy efficiency in drying is of obvious importance as energy consumption is such a large component of drying costs. Basically it is a simple ratio of the minimum energy needed to the energy actually consumed. But because of the complex relationships of the food, the water, and the drying medium which is often air, a number of efficiency measures can be worked out, each appropriate to circumstances and therefore selectable to bring out special features important in the particular process. Efficiency calculations are useful when assessing the performance of a dryer, looking for improvements, and in making comparisons between the various classes of dryers which may be alternatives for a particular drying operation.

Heat has to be supplied to separate the water from the food. The minimum quantity of heat that will remove the required water is that needed to supply the latent heat of evaporation, so one measure of efficiency is the ratio of that minimum to the energy actually provided for the process. Sensible heat can also be added to the minimum, as this added heat in the food often cannot be economically recovered.

Yet another useful measure for air drying such as in spray dryers, is to look at a heat balance over the air, treating the dryer as adiabatic with no exchange of heat with the surroundings. Then the useful heat transferred to the food for its drying corresponds to the drop in temperature in the drying air, and the heat which has to be supplied corresponds to the rise of temperature of the air in the air heater. So this adiabatic air-drying efficiency, h, can be defined by:

h = (T₁ - T₂)/(T₁ - T_a)                                                                                         (7.2)

where T₁ is the inlet (high) air temperature into the dryer, T₂ is the outlet air temperature from the dryer, and T_a is the ambient air temperature. The numerator, the gap between T₁ and T₂, is a major factor in the efficiency.

EXAMPLE 7.4. Efficiency of a potato dryer
A dryer reduces the moisture content of 100 kg of a potato product from 80% to 10% moisture. 250 kg of steam at 70 kPa gauge is used to heat 49,800 m³ of air to 80°C, and the air is cooled to 71°C in passing through the dryer. Calculate the efficiency of the dryer. The specific heat of potato is 3.43 kJ kg^-1 °C^-1. Assume potato enters at 24°C, which is also the ambient air temperature, and leaves at the same temperature as the exit air.

In 100 kg of raw material there is 80% moisture, that is 80 kg water and 20 kg dry material,
total weight of dry product = 20 x (10/9)
                                      = 22.2 kg
               weight of water = (22.2 - 20)
                                      = 2.2 kg.
                water removed = (80 - 2.2)
                                       = 77.8 kg.

Heat supplied to potato product
= sensible heat to raise potato product temperature from 24°C to 71°C + latent heat of vaporization.

Now, the latent heat of vaporization corresponding to a saturation temperature of 71°C is 2331 kJ kg^-1
Heat (minimum) supplied/100 kg potato
                                       = 100 x (71 - 24) x 3.43 + 77.8 x 2331
                                       = 16 x 10³ + 181 x 10³
                                       = 1.97 x 10⁵ kJ.
Heat to evaporate water only = 77.8 x 2331
                                       = 1.81 x 10⁵ kJ

The specific heat of air is 1.0 J kg^-1 °C^-1 and the density of air is 1.06 kg m^{-3 (Appendix 3)}
        Heat given up by air/100 kg potato
                                              = 1.0 x (80 - 71) x 49,800 x 1.06
                                              = 4.75 x 10⁵ kJ.

The latent heat of steam at 70 kPa gauge is 2283 kJ kg^-1
                          Heat in steam = 250 x 2283
                                              = 5.71 x 10⁵ kJ.

Therefore (a) efficiency based on latent heat of vaporisation only:
                                              = (1.81 x 10⁵)/ (5.71 x 10⁵)
                                              = 32%
              (b) efficiency assuming sensible heat remaining in food after drying is unavailable
                                              = (1.97 x 10⁵)/ (5.71 x 10⁵)
                                              = 36%
               (c) efficiency based heat input and output, in drying air
                                              = (80 – 71)/ (80 – 24)
                                              = 16%

Whichever of these is chosen depends on the objective for considering efficiency. For example in a spray dryer, the efficiency calculated on the air temperatures shows clearly and emphatically the advantages gained by operating at the highest feasible air inlet temperature and the lowest air outlet temperatures that can be employed in the dryer.

Examples of overall thermal efficiencies are:
              drum dryers 35-80%
              spray dryers 20-50%
              radiant dryers 30-40%

After sufficient energy has been provided to vaporize or to sublime moisture from the food, some way must be found to remove this moisture. In freeze-drying and vacuum systems it is normally convenient to condense the water to a liquid or a solid and then the vacuum pumps have to handle only the non-condensible gases. In atmospheric drying a current of air is normally used.


Drying > MASS TRANSFER IN DRYING

Back to the top