In
many cases, a substantial part of the water is found to be loosely bound.
This water can, for drying purposes, be considered as free water at the
surface. A comparison of the drying rates of sand, a material with mostly
free water, with meat containing more bound water shows the effect of
the binding of water on drying rates. Drying rate curves for these
are shown in Fig. 7.5.
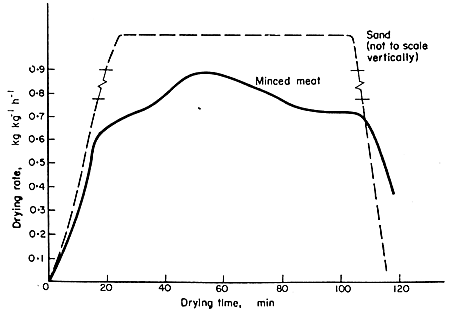
FIG. 7.5 Drying rate curves
The behaviour in which the drying behaves as though the water were at
a free surface, is called constant-rate drying. If w is the mass of the
material being dried then for constant rate drying:
dw/dt
= constant.
However
in food, unlike impervious materials such as sand, after a period of drying
at a constant rate it is found that the water then comes off more slowly.
A complete drying curve for fish, adapted from Jason
(1958), is shown in Fig. 7.6. The drying temperature
was low and this accounts for the long drying time.
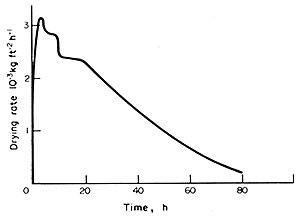
Figure 7.6 Drying curve for fish
A more generalized drying curve plotting the rate of drying as a percentage
of the constant (critical) rate, against moisture content, is shown in
Fig. 7.7.
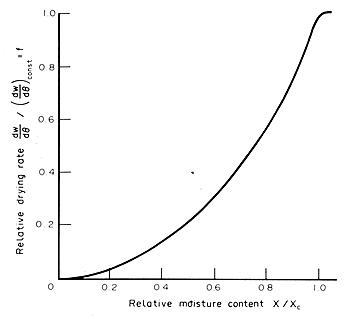
Figure 7.7 Generalized drying curve
The change from constant drying rate to a slower rate occurs at different
moisture contents for different foods. However, for many foods the change
from constant drying rate occurs at a moisture content in equilibrium
with air of 58-65% relative humidity, that is at aw
= 0.58-0.65. The moisture content at which this change of rate occurs
is known as the critical moisture content, Xc .
Another
point of importance is that many foods such as potato do not show a true
constant rate drying period. They do, however, often show quite a sharp
break after a slowly and steadily declining drying rate period and the
concept of constant rate is still a useful approximation.
The
end of the constant rate period, when X = Xc
at the break point of drying-rate curves, signifies that the water has
ceased to behave as if it were at a free surface and that factors other
than vapour-pressure differences are influencing the rate of drying. Thereafter
the drying rate decreases and this is called the falling-rate
period of drying. The rate-controlling factors in the falling-rate period
are complex, depending upon
diffusion through the food, and upon the changing energy-binding pattern
of the water molecules. Very little theoretical information is available
for drying of foods in this region and experimental drying curves are
the only adequate guide to design.
Calculation of Constant Drying Rates
In the constant-rate
period, the water is being evaporated from what is effectively a free
water surface. The rate of removal of water can then be related to the
rate of heat transfer, if there is no change in the temperature of the
material and therefore all heat energy transferred to it must result in
evaporation of water. The rate of removal of the water is also the rate
of mass transfer, from the solid to the ambient air. These two - mass
and heat transfer - must predict the same rate of drying for a given set
of circumstances.
Considering
mass transfer, which is fundamental to drying, the driving force is the
difference of the partial water vapour pressure between the food and the
air. The extent of this difference can be obtained, knowing the temperatures
and the conditions, by reference to tables or the psychrometric chart.
Alternatively, the driving force may be expressed in terms of humidity
driving forces and the numerical values of the mass-transfer coefficients
in this case are linked to the others through the partial pressure/humidity
relationships such as eqns. (7.4) and (7.5).
 EXAMPLE
7.13. Rate of evaporation on drying
The mass-transfer coefficient from a free water surface to an adjacent
moving air stream has been found to be 0.015 kg m-2 s-1.
Estimate the rate of evaporation from a surface of 1 m2 at
a temperature of 28°C into an air stream with a dry-bulb temperature
of 40°C and RH of 40% and the consequent necessary rate of supply
of heat energy to effect this evaporation.
From charts, the
humidity of saturated air at 40°C is 0.0495 kg kg-1.
Humidity of air at 40°C and 40%RH = 0.0495 x 0.4
= 0.0198 kg kg-1
=
Ya
From charts, the
humidity of saturated air at 28°C is 0.0244 kg kg-1 = Ys
Driving force
= (Ys -
Ya )
= (0.0244 - 0.0198) kg kg-1
= 0.0046 kg kg-1
Rate of evaporation
= k'gA(Ys - Ya)
= 0.015 x 1 x 0.0046
= 6.9 x 10-5 kg s-1
Latent heat of evaporation
of water at 28°C = 2.44 x 103 kJ kg-1
Heat energy supply
rate per square metre = 6.9 x 10-5 x 2.44 x 103
kJ s-1
=
0.168 kJ s-1
= 0.168 kW.
The problem in applying such apparently simple relationships to provide
the essential rate information for drying, is in the prediction of the
mass transfer coefficients. In the section on heat transfer, methods and
correlations were given for the prediction of heat transfer coefficients.
Such can be applied to the drying situation and the heat transfer rates
used to estimate rates of moisture removal. The reverse can also be applied.
EXAMPLE
7.14. Heat transfer in air drying
Using the data from Example 7.13, estimate the heat transfer coefficient
needed from the air stream to the water surface.
Heat-flow rate =
q = 168 J s
-1 from Example 7.13.
Temperature difference = dry-bulb temperature of air - wet-bulb temperature
(at food surface)
= (40
- 28)
= 12°C
= (Ta - Ts )
Since
q = hcA
(Ta - Ts)
from
Eqn (7.1)
168
= hc x 1 x 12
hc
= 14 J m-2 s-1 °C-1
Mass balances are
also applicable, and can be used, in drying and related calculations.
EXAMPLE
7.15. Temperature and RH in air drying of carrots
In a low-temperature drying situation, air at 60°C and 10 % RH is
being passed over a bed of diced carrots at the rate of 20 kg dry air
per second. If the rate of evaporation of water from the carrots, measured
by the rate of change of weight of the carrots, is 0.16 kg s-1
estimate the temperature and RH of the air leaving the dryer.
From
the psychrometric chart
Humidity of air at 60°C and 10%RH
= 0.013 kg kg-1.
Humidity added to air in drying
= 0.16 kg/20 kg dry air
=
0.008 kg kg-1
Humidity of air leaving dryer
=
0.013 + 0.008
=
0.021 kg kg-1
Following
on the psychrometric chart the wet-bulb line from the entry point at 60°C
and 10%RH up to the intersection of that line with a constant humidity
line of 0.021 kg kg-1, the resulting temperature is 41°C
and the RH 42%.
Because
the equations for predicting heat-transfer coefficients, for situations
commonly encountered, are extensive and much more widely available than
mass-transfer coefficients, the heat-transfer rates can be used to estimate
drying rates, through the Lewis ratio.
Remembering that (Le) = (hc/csk'g)
= 1 for the air/water system,from Eqn (7.5)
(strictly speaking the Lewis number, which arises in gaseous diffusion
theory, is (hc/k'gcp)
but for air of the humidity encountered in ordinary practice cs
»cp
»1.02
kJ kg-1 °C-1), therefore numerically, if hc
is in J m-2 s-1 °C -1, and k'g
in kg m-2 s-1, k'g = hc/1000,
the values of hc can be predicted using the standard
relationships for heat-transfer coefficients which have been discussed
in Chapter 4.
EXAMPLE
7.16. Lewis relationship in air drying
In Example 7.13 a value for k'g of 0.0150 kg m-2
s-1 was used. It was also found that the corresponding heat-transfer
coefficient for this situation was 15 J m-2 s-1
°C-1 as calculated in Example 7.14. Does this agree with
the expected value from the Lewis relationship (eqn. 7.5) for the air/water
system?
hc = 15 J m-2 s-1 °C-1
= 1000 x 0.0150
= 1000 x k'g as
the Lewis relationship predicts.
A
convenient way to remember the inter-relationship is that the mass transfer
coefficient from a free water surface into air expressed in g m-2
s-1 is numerically approximately equal to the heat-transfer
coefficient from the air to the surface expressed in J m-2
s-1 °C-1.
Falling rate Drying
The
highest rate of drying is normally the constant rate situation, then as
drying proceeds the moisture content falls and the access of water from
the interior of the food to the surface affects the rate and decreases
it. The situation then is complex with moisture gradients controlling
the observed drying rates. Actual rates can be measured, showing in the
idealized case a constant rate continuing up to the critical moisture
content and thereafter a declining rate as the food, on continued drying,
approaches the equilibrium moisture content for the food. This is clearly
shown by the drying curve of Fig. 7.7 and at low moisture contents the
rates of drying become very low. The actual detail of such curves depends,
of course, on the specific material and conditions of the drying process.
Calculation of Drying Times
Drying rates, once determined experimentally or predicted from theory,
can then be used to calculate drying times so that drying equipment and
operations can be designed. In the most general cases, the drying rates
vary throughout the dryer with time as drying proceeds, and with the changing
moisture content of the material. So the situation is complicated. However,
in many cases a simplified approach can provide useful results. One simplification
is to assume that the temperature and RH of the drying air are constant.
In
this case, for the constant-rate period, the time needed to remove the
quantity of water which will reduce the food material to the critical
moisture content Xc (that corresponding to the end
of the constant-rate period and below which the drying rate falls) can
be calculated by dividing this quantity of moisture by the rate.
So
t =
w (Xo- Xc) / (dw
/dt)const.
(7.6)
where
(dw /dt )const. = k'gA(Ys
-Ya)
and
Xo is the initial moisture content and Xc
the final moisture content (the critical moisture content in this case)
both on a dry basis, w is the amount of dry material in the food
and (dw/dt )const is the constant-drying rate.
Where
the drying rate is reduced by a factor f then this can be incorporated
to give:
Dt
= w (DX)/
f(dw /dt)const.
(7.7)
and
this has to be integrated piecemeal down to X = Xf where subscript
f denotes the final water content, and f expresses the ratio of
the actual drying rate to the maximum drying rate corresponding to the
free surface-moisture situation.
EXAMPLE
7.17. Time for air drying at constant rate
100 kg of food material are dried from an initial water content of 80%
on a wet basis and with a surface area of 12 m2. Estimate the
time needed to dry to 50% moisture content on a wet basis, assuming constant-rate
drying in air at a temperature of 120°C dry bulb and 50°C wet
bulb.
Under the conditions in the dryer, measurements indicate the heat-transfer
coefficient to the food surface from the air to be 18 J m-2
s-1 °C-1.
From the data
Xo
= 0.8/(1 - 0.8) = 4 kg kg-1,
Xf = 0.5/(1 - 0.5) = 1 kg kg-1,
and from the psychrometric
chart, Ys = 0.087 and Ya = 0.054 kg
kg-1
From the Lewis
relationship (Eqn. 7.5) k'g = 18 g m-2
s-1 = 0.018 kg m-2
w = 100(1 - 0.8) = 20 kg
Now we have
(dw /dt )const. = k'gA(Ys
-Ya)
and so t
= w ( Xo - Xf) / [k'gA(Ys
-Ya)]
(Using eqn. (7.3)
t = 20(4 - 1)/[0.018 x 12 x (0.087 - 0.054)]
= 60/7.128 x 10
= 8417 s
= 2.3 h (to remove 60 kg of water).
During
the falling-rate period, the procedure outlined above can be extended,
using the drying curve for the particular material and the conditions
of the dryer. Sufficiently small differential quantities of moisture content
to be removed have to be chosen, over which the drying rate is effectively
constant, so as to give an accurate value of the total time. As the moisture
content above the equilibrium level decreases so the drying rates decrease,
and drying times become long.
EXAMPLE
7.18. Time for drying during falling rate
Continuing Example 7.17, for the particular food material, the critical
moisture content, Xc, is 100% and the equilibrium
moisture content under the conditions in the dryer is 15% and the drying
curve is that illustrated in Fig. 7.7. Estimate the total time to dry
down to 17%, all moisture contents being on a dry basis.
Equation
(7.7) Dt
= w ( DX)
/ [f(dw /dt)const]
can
be applied, over small intervals of moisture content and multiplying the
constant rate by the appropriate reduction factor (f) read of
from Fig. 7.7. This can be set out in a table. Note the temperature and
humidity of the air were assumed to be constant throughout the drying.
| Moisture
content X |
0.5
|
|
0.4
|
|
0.3
|
|
0.2
|
|
0.18
|
|
0.17
|
| w(X1
- X2) |
|
2
|
|
2
|
|
2
|
|
0.4
|
|
0.2
|
|
| f |
|
0.86
|
|
0.57
|
|
0.29
|
|
0.11
|
|
0.005
|
|
1/f(dw/dt)const.
= 1/ f(7.128 x 10-3) |
|
1.63
x 102
|
|
2.46
x102
|
|
4.84
x 102
|
|
1.28
x 103
|
|
2.81
x 104
|
|
| t |
|
326
|
|
492
|
|
968
|
|
512
|
|
5620
|
|
St
= 7918 s = 2.2 h (to remove 6.6 kg of water) = time at falling rate
Therefore total drying time = (2.3 + 2.2) h = 4.5 h.
The example shows how as the moisture level descends toward the equilibrium
value so the drying rate becomes slower and slower. In terms of the mass
transfer equations, the humidity or partial pressure driving force is
tending to zero as the equilibrium moisture content is approached. In
terms of the heat transfer equations, the surface temperature rises above
the wet-bulb temperature once the surface ceases to behave as a wet surface.
The surface temperature then climbs towards the dry-bulb temperature of
the air as the moisture level continues to fall, thus leading to a continuously
diminishing temperature driving force for surface heat transfer.
This
calculation procedure can be applied to more complicated dryers, considering
them divided into sections, and applying the drying rate equations and
the input and output conditions to these sections sequentially to build
up the whole situation in the dryer.
 Drying
> CONDUCTION DRYING
 Back
to the top |
Calculation
of Constant Drying Rates 