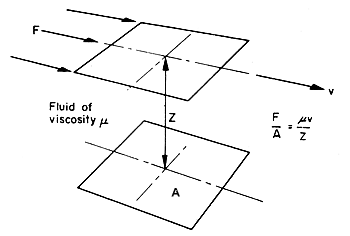
Figure 3.5. Viscous forces in a fluid.
If
the plane elements are at a distance Z apart, and if their relative
velocity is v, then the force F required to maintain the
motion has been found, experimentally, to be proportional to v
and inversely proportional to Z for many fluids. The coefficient of proportionality
is called the viscosity of the fluid, and it is denoted by the symbol
m
(mu).
From the definition
of viscosity we can write
F/A = mv/Z
(3.14)
where F
is the force applied, A is the area over which force is applied,
Z is the distance between planes, v is the velocity
of the planes relative to one another, and m
is the viscosity.
By rearranging the eqn. (3.14), the dimensions of viscosity can be found.
 |
[m]
= |
FZ
|
=
|
[F][L][t]
|
=
|
[F][t]
|
|
|
|
|
|
Av
|
[L2][L]
|
[L]2
|
= [M][L]-1[t]-1
There is some ambivalence
about the writing and the naming of the unit of viscosity; there is no
doubt about the unit itself which is the N s m-2, which is
also the Pascal second, Pa s, and it can be converted to mass units using
the basic mass/force equation. The older units, the poise and its sub-unit
the centipoise, seem to be obsolete, although the conversion is simple
with 10 poises or 1000 centipoises being equal to 1 N s m-2,
and to 1 Pa s.
The new unit is rather large for many liquids, the viscosity of water
at room temperature being around 1 x 10-3 N s m-2
and for comparison, at the same temperature, the approximate viscosities
of other liquids are acetone, 0.3 x 10-3 N s m-2;
a tomato pulp, 3 x 10-3; olive oil, 100 x 10-3;
and molasses 7000 N s m-2.
Viscosity is very dependent on temperature decreasing sharply as the temperature
rises. For example, the viscosity of golden syrup is about 100 N s m-2
at 16°C, 40 at 22°C and 20 at 25°C. Care should be taken not
to confuse viscosity m
as defined in eqn. (3.14) which strictly is called the dynamic or absolute
viscosity, with m/r
which is called the kinematic viscosity and given another symbol. In technical
literature, viscosities are often given in terms of units that are derived
from the equipment used to measure the viscosities experimentally. The
fluid is passed through some form of capillary tube or constriction and
the time for a given quantity to pass through is taken and can be related
to the viscosity of the fluid. Tables are available to convert these arbitrary
units, such as "Saybolt Seconds" or "Redwood Seconds",
to poises.
The
viscous properties of many of the fluids and plastic materials that must
be handled in food processing operations are more complex than can be
expressed in terms of one simple number such as a coefficient of viscosity.
Newtonian and Non-Newtonian Fluids
From the fundamental
definition of viscosity in eqn. (3.14) we can write:
F/A = mv
/Z = m
(dv/dz) = t
where
t
(tau) is called the shear stress in the fluid. This is an equation originally
proposed by Newton and which is obeyed by fluids such as water. However,
for many of the actual fluids encountered in the food industry, measurements
show deviations from this simple relationship, and lead towards a more
general equation:
t
= k(dv/dz)n
(3.15)
which can be called
the power-law equation, and where k is a constant of proportionality.
Where
n = 1 the fluids are called Newtonian because they conform to Newton's
equation (3.14) and k = m;
and all other fluids may therefore be called non-Newtonian. Non-Newtonian
fluids are varied and are studied under the heading of rheology, which
is a substantial subject in itself and the subject of many books. Broadly,
the non-Newtonian fluids can be divided into:
(1)
Those in which n < 1. As shown in Fig. 3.6 these
produce a concave downward curve and for them the viscosity is apparently
high under low shear forces decreasing as the shear force increases. Such
fluids are called pseudoplastic, an example being tomato puree. In more
extreme cases where the shear forces are low there may be no flow at all
until a yield stress is reached after which flow occurs, and these fluids
are called thixotropic.
(2)
Those in which n > 1. With a low apparent viscosity under
low shear stresses, they become more viscous as the shear rate rises.
This is called dilatancy and examples are gritty slurries such as crystallized
sugar solutions. Again there is a more extreme condition with a zero apparent
viscosity under low shear and such materials are called rheopectic. Bingham
fluids have to exceed a particular shear stress level (a yield stress)
before they start to move.
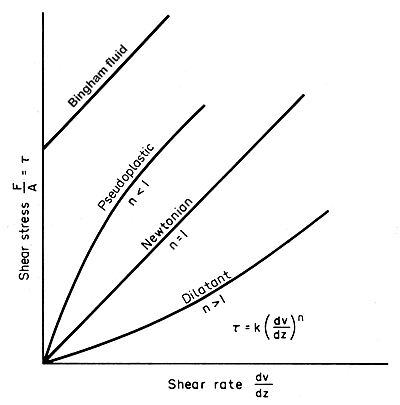
Figure 3.6. Shear stress/shear rate relationships in liquids.
In
many instances in practice non-Newtonian characteristics are important,
and they become obvious when materials that it is thought ought to pump
quite easily just do not. They get stuck in the pipes, or overload the
pumps, or need specially designed fittings before they can be moved. Sometimes
it is sufficient just to be aware of the general classes of behaviour
of such materials. In other cases it may be necessary to determine experimentally
the rheological properties of the material so that equipment and processes
can be adequately designed.
For further details see, for example, Charm (1971),
Steffe (2000).
 Fluid-flow
theory > STREAMLINE & TURBULENT FLOW
 Back
to the top |
Newtonian
and Non-Newtonian Fluids