Now,
the heat being lost from the surface must be transferred to the surface
from the interior of the cylinder by conduction. This heat transfer from
the interior to the surface is difficult to determine but as an approximation,
we can consider that all the heat is being transferred from the centre
of the cylinder. In this instance, we evaluate the temperature drop required
to produce the same rate of heat flow from the centre to the surface as
passes from the surface to the air. This requires a greater temperature
drop than the actual case in which much of the heat has in fact a shorter
path.
Assuming
that all the heat flows from the centre of the cylinder to the outside,
we can write the conduction equation
dQ/dt = (k/L)A( Tc–
Ts )
where Tc
is the temperature at the centre of the cylinder, k is the thermal
conductivity of the material of the cylinder and L is the radius
of the cylinder.
Equating these rates:
hsA(Ts --Ta)
= (k/L)A( Tc– Ts
)
hs(Ts
-- Ta) = (k/L)( Tc–
Ts )
and so hsL/k
= ( Tc– Ts )/ (Ts
-- Ta)
To
take a practical case of a copper cylinder of 15 cm radius cooling in
air kc = 380 J m-1 s-1 °C-1,
hs = 30 J m-2 s-1°C-1
(from Table 5.1), L = 0.15 m,
(Tc–
Ts)/ (Ts -- Ta)
= (30 x 0.15)/380
= 0.012
In
this case 99% of the temperature drop occurs between the air and the cylinder
surface. By comparison with the temperature drop between the surface of
the cylinder and the air, the temperature drop within the cylinder can
be neglected. On the other hand, if the cylinder were made of a poorer
conductor as in the case of the sausage, or if it were very large in diameter,
or if the surface heat-transfer coefficient were very much larger, the
internal temperature drops could not be neglected.
This simple analysis
shows the importance of the ratio:
|
heat
transfer coefficient at the surface
|
=
hsL/k
|
 |
 |
|
heat
conductance to the centre of the solid
|
|
This
dimensionless ratio is called the Biot number (Bi) and it is important
when considering unsteady state heat flow. When (Bi) is small, and for
practical purposes this may be taken as any value less than about 0.2,
the interior of the solid and its surface may be considered to be all
at one uniform temperature. In the case in which (Bi) is less than 0.2,
a simple analysis can be used, therefore, to predict the rate of cooling
of a solid body.
Therefore for a cylinder
of a good conductor, being cooled in air,
dQ = hsA(Ts
-- Ta) dt
But this loss of heat cools the cylinder in accordance with the usual
specific heat equation:
dQ = crVdT
where
c is the specific heat of the material of the cylinder, r
is the density of this material and V is the volume of the cylinder.
Since
the heat passing through the surface must equal the heat lost from the
cylinder, these two expressions for dQ can be equated:
crVdT
= hsA(Ts -- Ta)
dt
Integrating
between Ts = T1 and Ts
= T2 , the initial and final temperatures of the cylinder
during the cooling period, t, we have:
- hsAt/crV
= loge (T2 - Ta)/(T1–
Ta)
or (T2
- Ta)/(T1 – Ta)
= exp( -hsAt/crV
)
(5.6)
For this case, the temperatures for any desired interval can be calculated,
if the surface transfer coefficient and the other physical factors are
known. This gives a reasonable approximation so long as (Bi) is less than
about 0.2. Where (Bi) is greater than 0.2, the centre of the solid will
cool more slowly than this equation suggests. The equation is not restricted
to cylinders, it applies to solids of any shape so long as the restriction
in (Bi), calculated for the smallest half-dimension, is obeyed.
Charts
have been prepared which give the temperature relationships for solids
of simple shapes under more general conditions of unsteady-state conduction.
These charts have been calculated from solutions of the conduction equation
and they are plotted in terms of dimensionless groups so that their application
is more general. The form of the solution is:
ƒ{(T
- T0)/( Ti - T0
)} = F{(kt/crL2)(hsL/k)}
(5.7)
where
ƒ and F indicate functions of the terms following, Ti
is the initial temperature of the solid, T0 is the
temperature of the cooling or heating medium, T is the temperature
of the solid at time t, (kt/crL2)
is called the Fourier number (Fo) (this includes the
factor k/cr
the thermal conductance divided by the volumetric heat capacity, which
is called the thermal diffusivity) and (hsL/k)
is the Biot number.
A
mathematical outcome that is very useful in these calculations connects
results for two- and three-dimensional situations with results from one-dimensional
situations. This states that the two- and three-dimensional values called
F(x,y) and F(x,y,z) can be obtained
from the individual one-dimensional results if these are F(x),
F(y) and F(z), by simple multiplication:
F(x,y) = F(x)F(y)
and
F(x,y,z) = F(x)F(y)F(z)
Using the above result, the solution for the cooling or heating of a brick
is obtained from the product of three slab solutions. The solution for
a cylinder of finite length, such as a can, is obtained from the product
of the solution for an infinite cylinder, accounting for the sides of
the can, and the solution for a slab, accounting for the ends of the can.
Charts
giving rates of unsteady-state heat transfer to the centre of a slab,
a cylinder, or a sphere, are given in Fig. 5.4. On one
axis is plotted the fractional unaccomplished temperature change,
(T - T0)/( Ti - T0
). On the other axis is the Fourier number, which may be thought of in
this connection as a time coordinate. The various curves are for different
values of the reciprocal of the Biot number, k/hr for spheres and cylinders,
k/hl for slabs.
More detailed charts, giving surface and mean temperatures in addition
to centre temperatures, may be found in McAdams
(1954), Fishenden and Saunders (1950)
and Perry (1997).
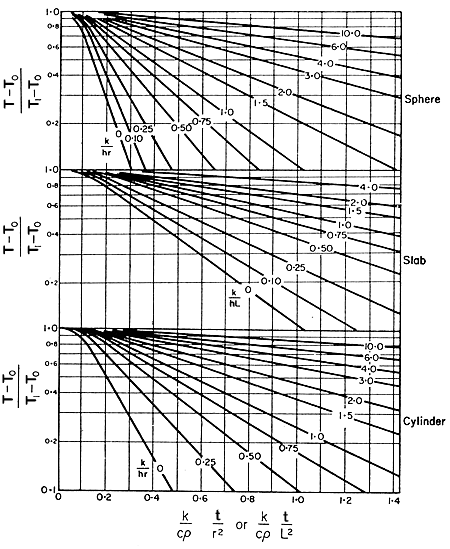
Figure 5.4. Transient heat conduction
Temperatures at the centre of sphere,slab,and cylinder: adapted
from Henderson and Perry, Agricultural Process Engineering, 1955
 EXAMPLE
5.5. Heat transfer in cooking sausages EXAMPLE
5.5. Heat transfer in cooking sausages
A process is under consideration in which large cylindrical meat sausages
are to be processed in an autoclave. The sausage may be taken as thermally
equivalent to a cylinder 30 cm long and 10 cm in diameter. If the sausages
are initially at a temperature of 21°C and the temperature in the
autoclave is maintained at 116°C, estimate the temperature of the
sausage at its centre 2 h after it has been placed in the autoclave.
Assume that the thermal conductivity of the sausage is 0.48 J m-1
s-1 °C-1, that its specific gravity is 1.07,
and its specific heat is 3350 J kg-1 °C-1. The
surface heat-transfer coefficient in the autoclave to the surface of the
sausage is 1200 J m-2 s-1 °C-1.
This
problem can be solved by combining the unsteady-state solutions for a
cylinder with those for a slab, working from Fig. 5.3.
(a) For the cylinder,
of radius r = 5 cm (instead of L in this case)
Bi = hsr/k
= (1200 x 0.05)/0.48 = 125
(Often
in these systems the length dimension used as parameter in the charts
is the half-thickness, or the radius, but this has to be checked on the
graphs used.)
So
1/(Bi) = 8 x 10-3
After 2 hours
t = 7200 s
Therefore Fo = kt/crr2
= (0.48 x 7200)/[3350 x 1.07 x 1000 x (0.05)2] = 0.39
and so from Fig.
5.3 for the cylinder:
(T - T0)/( Ti - T0
) = 0.175 = say, F(x).
(b) For the slab
the half-thickness 30/2 cm = 0.15 m
and so Bi = hsL/k = (1200 x 0.15)/0.48
= 375
1/ Bi = 2.7 x 10-3
t = 7200 s as before and
kt/crL2
= (0.48 x 7200)/[3350 x 1.07 x 1000 x (0.15)2]
=
4.3 x 10-2
and so from Fig.
5.3 for the slab:
(T - T0)/( Ti - T0
) = 0.98 = say, F(y)
So overall (T
- T0)/( Ti - T0
) = F(x) F(y)
= 0.175 x 0.98
= 0.172
| Therefore |
T2
- 116
|
=
0.172
|
 |
 |
 |
| |
21
- 116
|
|
Therefore
T2 = 100°C
 Heat-Transfer
Theory > RADIATION-HEAT TRANSFER Heat-Transfer
Theory > RADIATION-HEAT TRANSFER
 Back
to the top Back
to the top |

