Unit Operations in Food Processing

Food liquid mixtures could in theory be sampled and analysed in the same way as solid mixtures but little investigational work has been published on this, or on the mixing performance of fluid mixers. Most of the information that is available concerns the power requirements for the most commonly used liquid mixer - some form of paddle or propeller stirrer. In these mixers, the fluids to be mixed are placed in containers and the stirrer is rotated. Measurements have been made in terms of dimensionless ratios involving all of the physical factors that influence power consumption. The results have been correlated in an equation of the form

(Po) = K(Re)ⁿ(Fr)^m (12.7)

where (Re) = (D²Nr/m), (Po) = (P/D⁵N³r) and this is called the Power number (relating drag forces to inertial forces), (Fr) = (DN²/g) and this is called the Froude number (relating inertial forces to those of gravity); D is the diameter of the propeller, N is the rotational frequency of the propeller (rev/sec), r is the density of the liquid, m is the viscosity of the liquid and P is the power consumed by the propeller.

Notice that the Reynolds number in this instance, uses the product DN for the velocity, which differs by a factor of p from the actual velocity at the tip of the propeller.

The Froude number correlates the effects of gravitational forces and it only becomes significant when the propeller disturbs the liquid surface. Below Reynolds numbers of about 300, the Froude number is found to have little or no effect, so that eqn. (12.7) becomes:

(Po) = K(Re)ⁿ (12.8)

Experimental results from the work of Rushton are shown plotted in Fig. 12.1.

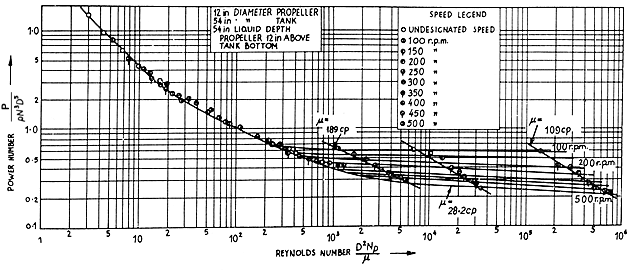
FIG. 12.1 Performance of propeller mixers
Figure 12.1 Performance of propeller mixers
Adapted from Rushton (1950)

Unfortunately, general formulae have not been obtained, so that the results are confined to the particular experimental propeller configurations that were used. If experimental curves are available, then they can be used to give values for n and K in eqn. (12.8) and the equation then used to predict power consumption. For example, for a propeller, with a pitch equal to the diameter, Rushton gives n = -1 and K = 41.

In cases in which experimental results are not already available, the best approach to the prediction of power consumption in propeller mixers is to use physical models, measure the factors, and then use eqn. (12.7) or eqn. (12.8) for scaling up the experimental results.

EXAMPLE 12.6. Blending vitamin concentrate into molasses
Vitamin concentrate is being blended into molasses and it has been found that satisfactory mixing rates can be obtained in a small tank 0.67 m diameter, height 0.75 m,with a propeller 0.33 m diameter rotating at 450 rev min^-1. If a large-scale plant is to be designed which will require a tank 2 m diameter, what will be suitable values to choose for tank depth, propeller diameter and rotational speed, if it is desired to preserve the same mixing conditions as in the smaller plant? What would be the power requirement for the motor driving the propeller? Assume that the viscosity of molasses is 6.6 N s m^-2 and its density is 1520 kg m^-3.

Use the subscripts S for the small tank and L for the larger one. To preserve geometric similarity the dimensional ratios should be the same in the large tank as in the small.

Given that the full-scale tank is three times larger than the model,
D_L = 3D_S.

depth of large tank = H_L = 3H_S = 3 x 0.75 = 2.25 m
and
propeller diameter in the large tank = D_L = 3D_S = 3 x 0.33 = 1 m .

For dynamic similarity, (Re)_L = (Re)_S
(D²Nr/m)_L = (D²Nr/m)_S

  D_L²N_L = D_S²N_S

        N_L = (1/3)² x 450
             = 50 rev min^-1
             = 0.83 rev sec^-1.
             = speed of propeller in the large tank.

For the large tank (Re) = (D_L²N_Lr/m)

so (Re) = (1² x 0.83 x 1520)/6.6
= 191

Eqn. (12.8) is applicable, and assuming that K = 41 and n = -1, we have

      (Po) = 41(Re)^-1 = (P/D⁵N³r)

        P = (41 x 1⁵ x (0.83)³ x 1520)/(191)
             = 186 J s^-1

And since 1 horsepower = 746 J s^-1
Required motor = 186/746, say 1/4 horsepower.

Apart from deliberate mixing, liquids in turbulent flow or passing through equipment such as pumps are being vigorously mixed. By planning such equipment in flow lines, or by ensuring turbulent flow in pipelines, liquid mixing may in many instances be satisfactorily accomplished as a byproduct of fluid transport.

Mixing > MIXING EQUIPMENT

Back to the top