Grinding and cutting reduce the size of solid materials by mechanical
action, dividing them into smaller particles. Perhaps the most extensive
application of grinding in the food industry is in the milling of grains
to make flour, but it is used in many other processes, such as in the
grinding of corn for manufacture of corn starch, the grinding of sugar
and the milling of dried foods, such as vegetables.
Cutting
is used to break down large pieces of food into smaller pieces suitable
for further processing, such as in the preparation of meat for retail
sales and in the preparation of processed meats and processed vegetables.
In
the grinding process, materials are reduced in size by fracturing them.
The mechanism of fracture is not fully understood, but in the process,
the material is stressed by the action of mechanical moving parts in the
grinding machine and initially the stress is absorbed internally by the
material as strain energy. When the local strain energy exceeds a critical
level, which is a function of the material, fracture occurs along lines
of weakness and the stored energy is released. Some of the energy is taken
up in the creation of new surface, but the greater part of it is dissipated
as heat. Time also plays a part in the fracturing process and it appears
that material will fracture at lower stress concentrations if these can
be maintained for longer periods. Grinding is, therefore, achieved by
mechanical stress followed by rupture and the energy required depends
upon the hardness of the material and also upon the tendency of the material
to crack - its friability.
The force applied
may be compression, impact, or shear, and both the magnitude of the force
and the time of application affect the extent of grinding achieved. For
efficient grinding, the energy applied to the material should exceed,
by as small a margin as possible,
the minimum energy needed to rupture the material . Excess energy is lost
as heat and this loss should be kept as low as practicable.
The important factors
to be studied in the grinding process are the amount of energy used and
the amount of new surface formed by grinding.
Energy Used in Grinding
Grinding
is a very inefficient process and it is important to use energy as efficiently
as possible. Unfortunately, it is not easy to calculate the minimum energy
required for a given reduction process, but some theories have been advanced
which are useful.
These
theories depend upon the basic assumption that the energy required to
produce a change dL in a particle of a typical size dimension L
is a simple power function of L:
dE/dL
= KLn
(11.1)
where
dE is the differential energy required, dL is the change
in a typical dimension, L is the magnitude of a typical length
dimension and K, n, are constants.
Kick
assumed that the energy required to reduce a material in size was directly
proportional to the size reduction ratio dL/L. This implies that
n in eqn. (11.1) is equal to -1. If
K = KKfc
where KK is called Kick's constant
and fc is called the crushing strength of the material,
we have:
dE/dL = KKfcL-1
which, on integration gives:
E = KKfc
loge(L1/L2)
(11.2)
Equation
(11.2) is a statement of Kick's Law. It implies that the specific energy
required to crush a material, for example from 10 cm down to 5 cm, is
the same as the energy required to crush the same material from 5 mm to
2.5 mm.
Rittinger,
on the other hand, assumed that the energy required for size reduction
is directly proportional, not to the change in length dimensions, but
to the change in surface area. This leads to a value of -2 for n
in eqn. (11.1) as area is proportional to length squared. If we put:
K = KRfc
and so
dE/dL
= KRfcL-2
where KR is called Rittinger's constant,
and integrate the resulting form of eqn. (11.1), we obtain:
E = KRfc(1/L2–
1/L1)
(11.3)
Equation
(11.3) is known as Rittinger's Law. As the specific surface of a particle,
the surface area per unit mass, is proportional to 1/L, eqn. (11.3)
postulates that the energy required to reduce L for a mass of particles
from 10 cm to 5 cm would be the same as that required to reduce, for example,
the same mass of 5 mm particles down to 4.7 mm. This is a very much smaller
reduction, in terms of energy per unit mass for the smaller particles,
than that predicted by Kick's Law.
It
has been found, experimentally, that for the grinding of coarse particles
in which the increase in surface area per unit mass is relatively small,
Kick's Law is a reasonable approximation. For the size reduction of fine
powders, on the other hand, in which large areas of new surface are being
created, Rittinger's Law fits the experimental data better.
Bond has suggested an intermediate course, in which he postulates
that n is -3/2 and this leads to:
E = Ei (100/L2)1/2[1
- (1/q1/2)]
(11.4)
Bond
defines the quantity Ei by this equation: L is
measured in microns in eqn. (11.4) and so Ei is the
amount of energy required to reduce unit mass of the material from an
infinitely large particle size down to a particle size of 100 mm.
It is expressed in terms of q, the reduction ratio where q =
L1/L2.
Note
that all of these equations [eqns. (11.2), (11.3), and (11.4)] are dimensional
equations and so if quoted values are to be used for the various constants,
the dimensions must be expressed in appropriate units. In Bond's equation,
if L is expressed in microns, this defines Ei
and Bond calls this the Work Index.
The
greatest use of these equations is in making comparisons between power
requirements for various degrees of reduction.
 EXAMPLE
11.1. Grinding of sugar EXAMPLE
11.1. Grinding of sugar
Sugar is ground from crystals of which it is acceptable that 80% pass
a 500 mm
sieve(US Standard Sieve No.35), down to a size in which it is acceptable
that 80% passes a 88 mm
(No.170) sieve, and a 5-horsepower motor is found just sufficient for
the required throughput. If the requirements are changed such that the
grinding is only down to 80% through a 125 mm
(No.120) sieve but the throughput is to be increased by 50% would the
existing motor have sufficient power to operate the grinder? Assume Bond's
equation.
Using
the subscripts 1 for the first condition and 2 for the second, and letting
m kg h-1 be the initial throughput, then if x
is the required power
Now 88mm
= 8.8 x 10-6m , 125 mm
= 125 x 10-6m , 500mm
= 500 x 10-6m
E1 = 5/m = Ei(100/88 x 10-6)1/2
[1 – (88/500)1/2]
E2 = x/1.5m = Ei(100/125
x 10-6)1/2 [1 - (125/500)1/2]
E2/E1 = x/(1.5 x 5) =
(88 x 10-6)1/2[1 - (125/500)1/2]
(125 x 10-6)1/2[1 – (88/500)1/2]
x/(7.5) = 0.84 x (0.500/0.58)
= 0.72
x = 5.4 horsepower.
So
the motor would be expected to have insufficient power to pass the 50%
increased throughput, though it should be able to handle an increase of
40%.
New Surface Formed by Grinding
When
a uniform particle is crushed, after the first crushing the size of the
particles produced will vary a great deal from relatively coarse to fine
and even to dust. As the grinding continues, the coarser particles will
be further reduced but there will be less change in the size of the fine
particles. Careful analysis has shown that there tends to be a certain
size that increases in its relative proportions in the mixture and which
soon becomes the predominant size fraction. For example, wheat after first
crushing gives a wide range of particle sizes in the coarse flour, but
after further grinding the predominant fraction soon becomes that passing
a 250 mm
sieve and being retained on a 125 mm
sieve. This fraction tends to build up, however long the grinding continues,
so long as the same type of machinery, rolls in this case, is employed.
The
surface area of a fine particulate material is large and can be important.
Most reactions are related to the surface area available, so the surface
area can have a considerable bearing on the properties of the material.
For example, wheat in the form of grains is relatively stable so long
as it is kept dry, but if ground to a fine flour has such a large surface
per unit mass that it becomes liable to explosive oxidation, as is all
too well known in the milling industry. The surface area per unit mass
is called the specific surface. To calculate this in a known mass
of material it is necessary to know the particle-size distribution and,
also the shape factor of the particles. The particle size gives one dimension
that can be called the typical dimension, Dp, of a
particle. This has now to be related to the surface area.
We can write, arbitrarily:
Vp = pDp3
and
Ap= 6qDp2.
where
Vp is the volume of the particle, Ap
is the area of the particle surface, Dp is the typical
dimension of the particle and p, q are factors which connect the
particle geometries.(Note subscript p and factor p)
For
example, for a cube, the volume is Dp3 and
the surface area is 6Dp2; for a sphere the volume
is (p/6)Dp3
and the surface area is pDp2
In each case the ratio of surface area to volume is 6/Dp.
A
shape factor is now defined as q/p = l
(lambda), so that for a cube or a sphere l
= 1. It has been found, experimentally, that for many materials when ground,
the shape factor of the resulting particles is approximately 1.75, which
means that their surface area to volume ratio is nearly twice that for
a cube or a sphere.
The ratio of surface area to volume is:
Ap/Vp
=( 6q/p)Dp = 6l/Dp
(11.5)
and so Ap=
6q Vp/pDp = 6l(VP/DP)
If
there is a mass m of particles of density rp,
the number of particles is m/rpVP
each of area Ap.
So total area At
= (m/rpVP)
x ( 6qVp/pDP) =
6qm/rp
pDp
=
6lm/rDp
(11.6)
where
At is the total area of the mass of particles. Equation
(11.6) can be combined with the results of sieve analysis to estimate
the total surface area of a powder.
 EXAMPLE
11.2. Surface area of salt crystals EXAMPLE
11.2. Surface area of salt crystals
In an analysis of ground salt using Tyler sieves, it was found that 38%
of the total salt passed through a 7 mesh sieve and was caught on a 9
mesh sieve. For one of the finer fractions, 5% passed an 80 mesh sieve
but was retained on a 115 mesh sieve. Estimate the surface areas of these
two fractions in a 5 kg sample of the salt, if the density of salt is
1050 kg m-3 and the shape factor (l)
is 1.75.
Aperture
of Tyler sieves, 7 mesh = 2.83 mm, 9 mesh = 2.00 mm, 80 mesh = 0.177 mm,
115 mesh = 0.125 mm.
Mean aperture 7 and 9 mesh = 2.41 mm = 2.4
x 10-3m
Mean aperture 80 and 115 mesh = 0.151 mm = 0.151 x 10-3m
Now from Eqn. (11.6)
A1 = (6 x 1.75 x 0.38 x 5)/(1050 x 2.41 x 10-3)
= 7.88 m2
A2 = (6 x 1.75 x 0.05 x 5)/(1050
x 0.151 x 10-3)
= 16.6 m2.
Grinding Equipment
Grinding equipment can be divided into two classes - crushers and grinders.
In the first class the major action is compressive, whereas grinders combine
shear and impact with compressive forces.
Crushers
Jaw
and gyratory crushers are heavy equipment and are not used extensively
in the food industry. In a jaw crusher, the material is fed in between
two heavy jaws, one fixed and the other reciprocating, so as to work the
material down into a narrower and narrower space, crushing it as it goes.
The gyrator crusher consists of a truncated conical casing, inside which
a crushing head rotates eccentrically. The crushing head is shaped as
an inverted cone and the material being crushed is trapped between the
outer fixed, and the inner gyrating, cones, and it is again forced into
a narrower and narrower space during which time it is crushed. Jaw and
gyratory crusher actions are illustrated in Fig. 11.1(a) and (b).
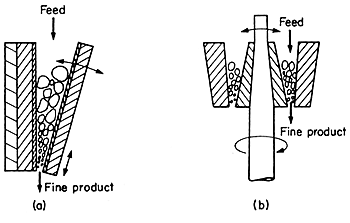
Figure 11.1 Crushers: (a) jaw, (b) gyratory
Crushing rolls consist of two horizontal heavy cylinders, mounted parallel
to each other and close together. They rotate in opposite directions and
the material to be crushed is trapped and nipped between them being crushed
as it passes through. In some case, the rolls are both driven at the same
speed. In other cases, they may be driven at differential speeds, or only
one roll is driven. A major application is in the cane sugar industry,
where several stages of rolls are used to crush the cane.
Hammer mills
In a hammer mill, swinging hammerheads are attached to a rotor that rotates
at high speed inside a hardened casing. The principle is illustrated in
Fig. 11.2(a).
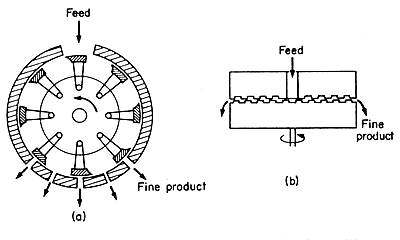
Figure 11.2 Grinders: (a) hammer mill, (b) plate mill
The material is crushed and pulverized between the hammers and the casing
and remains in the mill until it is fine enough to pass through a screen
which forms the bottom of the casing. Both brittle and fibrous materials
can be handled in hammer mills, though with fibrous material, projecting
sections on the casing may be used to give a cutting action.
Fixed head mills
Various
forms of mills are used in which the material is sheared between a fixed
casing and a rotating head, often with only fine clearances between them.
One type is a pin mill in which both the static and the moving plates
have pins attached on the surface and the powder is sheared between the
pins.
Plate mills
In
plate mills the material is fed between two circular plates, one of them
fixed and the other rotating. The feed comes in near the axis of rotation
and is sheared and crushed as it makes its way to the edge of the plates,
see Fig. 11.2(b). The plates can be mounted horizontally as in the traditional
Buhr stone used for grinding corn, which has a fluted surface on the plates.
The plates can be mounted vertically also. Developments of the plate mill
have led to the colloid mill, which uses very fine clearances and very
high speeds to produce particles of colloidal dimensions.
Roller mills
Roller
mills are similar to roller crushers, but they have smooth or finely fluted
rolls, and rotate at differential speeds. They are used very widely to
grind flour. Because of their simple geometry, the maximum size of the
particle that can pass between the rolls can be regulated. If the friction
coefficient between the rolls and the feed material is known, the largest
particle that will be nipped between the rolls can be calculated, knowing
the geometry of the particles.
Miscellaneous milling equipment
The
range of milling equipment is very wide. It includes ball mills, in which
the material to be ground is enclosed in a horizontal cylinder or a cone
and tumbled with a large number of steel balls, natural pebbles or artificial
stones, which crush and break the material. Ball mills have limited applications
in the food industry, but they are used for grinding food colouring materials.
The edge runner mill, which is basically a heavy broad wheel running round
a circular trough, is used for grinding chocolate and confectionery.
Many types of milling equipment have come to be traditional in various
industries and it is often claimed that they provide characteristic actions
that are peculiarly suited to, and necessary for, the product.
Cutters
Cutting
machinery is generally simple, consisting of rotating knives in various
arrangements. A major problem often is to keep the knives sharp so that
they cut rather than tear. An example is the bowl chopper in which a flat
bowl containing the material revolves beneath a vertical rotating cutting
knife.
 Size
Reduction > EMULSIFICATION Size
Reduction > EMULSIFICATION
 Back
to the top Back
to the top |
![]() Grinding
and cutting.
Grinding
and cutting. ![]() Energy Used in Grinding
Energy Used in Grinding![]() New Surface Formed by Grinding
New Surface Formed by Grinding![]() Grinding
equipment.
Grinding
equipment. ![]() Crushers
Crushers![]() Hammer mills
Hammer mills ![]() Fixed-head mills
Fixed-head mills ![]() Plate mills
Plate mills ![]() Roller mills
Roller mills ![]() Miscellaneous milling equipment
Miscellaneous milling equipment![]() Cutters
Cutters


