Studies
of the microorganisms that occur in foods, have led to the selection of
certain types of bacteria as indicator organisms. These are the most difficult
to kill, in their spore forms, of the types of bacteria which are likely
to be troublesome in foods.
A frequently used indicator organism is Clostridium botulinum.
This particular organism is a very important food poisoning organism as
it produces a deadly toxin and also its spores are amongst the most heat
resistant. Processes for the heat treatment of foodstuffs are therefore
examined with respect to the effect they would have on the spores of C.
botulinum. If the heat process would not destroy this organism then
it is not adequate. As C. botulinum is a very dangerous organism,
a selected strain of a non-pathogenic organism of similar heat resistance
is often used for testing purposes.
Thermal Death Time
It
has been found that microorganisms, including C. botulinum, are
destroyed by heat at rates which depend on the temperature, higher temperatures
killing spores more quickly. At any given temperature, the spores are
killed at different times, some spores being apparently more resistant
to heat than other spores. If a graph is drawn, the number of surviving
spores against time of holding at any chosen temperature, it is found
experimentally that the number of surviving spores fall asymptotically
to zero. Methods of handling process kinetics are well developed and if
the standard methods are applied to such results, it is found that thermal
death of microorganisms follows, for practical purposes, what is called
a first-order process at a constant temperature (see for example Earle
and Earle, 2003).
This implies that the fractional destruction in any fixed time interval,
is constant. It is thus not possible, in theory at least, to take the
time when all of the organisms are actually destroyed. Instead it is practicable,
and very useful, to consider the time needed for a particular fraction
of the organisms to be killed.
The
rates of destruction can in this way be related to:
(1) The numbers of viable organisms in the initial container or batch
of containers.
(2) The number of viable organisms which can safely be allowed to survive.
Of
course the surviving number must be small indeed, very much less than
one, to ensure adequate safety. However, this concept, which includes
the admissibility of survival numbers of much less than one per container,
has been found to be very useful. From such considerations, the ratio
of the initial to the final number of surviving organisms becomes the
criterion that determines adequate treatment. A combination of historical
reasons and extensive practical experience has led to this number being
set, for C. botulinum, at 1012:1. For other organisms,
and under other circumstances, it may well be different.
The
results of experiments to determine the times needed to reduce actual
spore counts from 1012 to 1 (the lower, open, circles) or to
0 (the upper, closed, circles) are shown in Fig. 6.4.
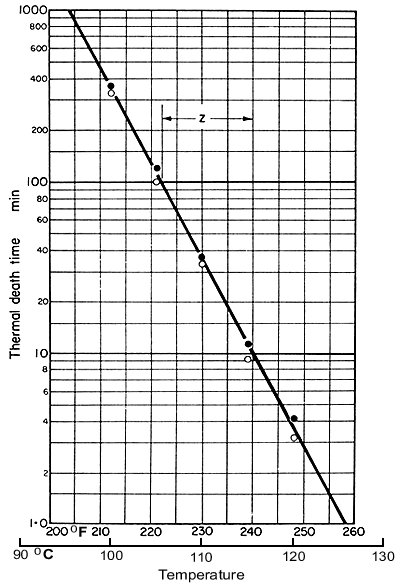
Figure 6.4. Thermal death time curve for Clostridium botulinum
Based on research results from the American Can
Company
In this graph, these
times are plotted against the different temperatures and it shows that
when the logarithms of these times are plotted against temperatures, the
resulting graph is a straight line. The mean times on this graph are called
thermal death times for the corresponding temperatures. Note that these
thermal death times do not represent complete sterilization, but a mathematical
concept which can be considered as effective sterilization, which is in
fact a survival ratio of 1:1012, and which has been found adequate
for safety
Any canning process must be considered then from the standpoint of effective
sterilization. This is done by combining the thermal death time data with
the time-temperature relationships at the point in the can that heats
slowest. Generally, this point is on the axis of the can and somewhere
close to the geometric centre. Using either the unsteady-state heating
curves or experimental measurements with a thermocouple at the slowest
heating point in a can, the temperature-time graph for the can under the
chosen conditions can be plotted. This curve has then to be evaluated
in terms of its effectiveness in destroying C. botulinum or any
other critical organism, such as thermophilic spore formers, which are
important in industry. In this way the engineering data, which provides
the temperatures within the container as the process is carried out, are
combined with kinetic data to evaluate the effect of processing on the
product.
Considering
Fig. 6.4, the standard reference temperature is generally selected as
121.1°C (250 °F), and the relative time (in minutes) required
to sterilize, effectively, any selected organism at 121°C is spoken
of as the F
value of that organism. In our example,
reading from Fig. 6.4, the F value is about 2.8 min. For any process
that is different from a steady holding at 121°C, our standard process,
the actual attained F values can be worked out by stepwise integration.
If the total F value so found is below 2.8 min, then sterilization
is not sufficient; if above 2.8 min, the heat treatment is more drastic
than it needs to be.
Equivalent Killing Power at Other Temperatures
The
other factor that must be determined, so that the equivalent killing powers
at temperatures different from 121°C can be evaluated, is the dependence
of thermal death time on temperature. Experimentally, it has been found
that if the logarithm of t, the thermal death time, is plotted
against the temperature, a straight-line relationship is obtained. This
is shown in Fig. 6.4 and more explicitly in Fig. 6.5.
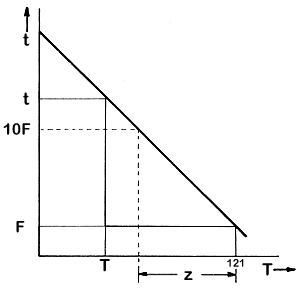
Figure 6.5 Thermal death time/temperature relationships
We can then write from the graph
log t - log
F = m(121 –T) = log t/F
where
t is the thermal death time at temperature T, F is the thermal
death time at temperature 121°C and m is the slope of the
graph.
Also,
if we define the z value as the number of degrees below
121°C at which t increases by a factor of 10, that is by
one cycle on a logarithmic graph,
t = 10F when T = (121 - z)
so that,
log 10F - logF = log (10F/F) = 1 = m[121 -
(121 - z)]
and so
z = 1/m
Therefore
log (t/F) = (121 - T)/z
or t = F x 10(121-T)/z
(6.3)
Now,
the fraction of the process towards reaching thermal death, dS,
accomplished in time dt is given by (1/t1)dt,
where t1 is the thermal death time at temperature T1,
assuming that the destruction is additive.
That is dS = (1/t1)dt
or = (1/F)10-(121-T)/z
dt
When the thermal
death time has been reached, that is when effective sterilization has
been achieved,
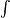 dS
= 1
that
is
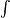(1/F)10-(121-T)/z
dt
= 1
or 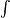10-(121-T)/z
dt
= F
(6.4)
This
implies that the sterilization process is complete, that the necessary
fraction of the bacteria/spores have been destroyed, when the integral
is equal to F. In this way, the factors F and z can
be combined with the time-temperature curve and integrated to evaluate
a sterilizing process.The integral can be evaluated graphically or
by stepwise numerical integration. In this latter case the contribution
towards F of a period of t min at a temperature T
is given by t x 10-(121-T)/z
Breaking up the temperature-time curve into t1
min at T1, t2 mm at T2,
etc., the total F is given by
F = t1 x 10-(121-T1)/z
+ t2 x 10-(121-T2)/z
+ …………..
This
value of F is then compared with the standard value of F
for the organism, for example 2.8 min for C. botulinum in our
example, to decide whether the sterilizing procedure is adequate.
 EXAMPLE
6.5. Time/Temperature in a can during sterilisation
In a retort, the temperatures in the slowest heating region of a can of
food were measured and were found to be shown as in Fig. 6.6. Is
the retorting adequate, if F for the process is 2.8 min and z
is 10°C?
Figure 6.6 Time/Temperature curve for can processing
Approximate
stepped temperature increments are drawn on the curve giving the equivalent
holding times and temperatures as shown in Table 6.2. The corresponding
F values are calculated for each temperature step.
TABLE
6.2
|
Temperature
T (°C)
|
Time
t (min)
|
(121 - T)
|
10-(121-T)/10
|
t x 10-(121-T)/10
|
|
80
|
11
|
41
|
7.9
x 10-5
|
0.00087
|
|
90
|
8
|
31
|
7.9
x 10-4
|
0.0063
|
|
95
|
6
|
26
|
2.5
x 10-3
|
0.015
|
|
100
|
10
|
21
|
7.9
x 10-3
|
0.079
|
|
105
|
12
|
16
|
2.5
x 10-2
|
0.30
|
|
108
|
6
|
13
|
5.0
x 10-2
|
0.30
|
|
109
|
8
|
12
|
6.3
x 10-2
|
0.50
|
|
110
|
17
|
11
|
7.9
x 10-2
|
1.34
|
|
107
|
2
|
14
|
4.0
x 10-2
|
0.08
|
|
100
|
2
|
21
|
7.9
x 10-3
|
0.016
|
|
90
|
2
|
31
|
7.9
x 10-4
|
0.0016
|
|
80
|
8
|
41
|
7.9
x 10-5
|
0.0006
|
|
70
|
6
|
51
|
7.9
x 10-6
|
0.00005
|
|
|
|
|
Total
|
2.64
|
The above results show that the F value for the process = 2.64
so that the retorting time is not quite adequate. This could be corrected
by a further 2 min at 110°C (and proceeding as above, this would add
2 x 10-(121-110)/10
= 0.16, to 2.64, making 2.8).
From
the example, it may be seen that the very sharp decrease of thermal death
times with higher temperatures means that holding times at the lower temperatures
contribute little to the sterilization. Very long times at temperatures
below 90°C would be needed to make any appreciable difference to F,
and in fact it can often be the holding time at the highest temperature
which virtually determines the F value of the whole process. Calculations
can be shortened by neglecting those temperatures that make no significant
contribution, although, in each case, both the number of steps taken and
also their relative contributions should be checked to ensure accuracy
in the overall integration.
It
is possible to choose values of F and of z to suit specific
requirements and organisms that may be suspected of giving trouble. The
choice and specification of these is a whole subject in itself and will
not be further discussed. From an engineering viewpoint a specification
is set, as indicated above, with an F value and a z value, and
then the process conditions are designed to accomplish this.
The
discussion on sterilization is designed to show, in an elementary way,
how heat-transfer calculations can be applied and not as a detailed treatment
of the topic. This can be found in appropriate books such as Stumbo
(1973), Earle and Earle (2003).
Pasteurization
Pasteurization
is a heat treatment applied to foods, which is less drastic than sterilization,
but which is sufficient to inactivate particular disease-producing organisms
of importance in a specific foodstuff. Pasteurization inactivates most
viable vegetative forms of microorganisms but not heat-resistant spores.
Originally, pasteurization was evolved to inactivate bovine tuberculosis
in milk. Numbers of viable organisms are reduced by ratios of the order
of 1015:1. As well as the application to inactivate bacteria,
pasteurization may be considered in relation to enzymes present in the
food, which can be inactivated by heat. The same general relationships
as were discussed under sterilization apply to pasteurization. A combination
of temperature and time must be used that is sufficient to inactivate
the particular species of bacteria or enzyme under consideration. Fortunately,
most of the pathogenic organisms, which can be transmitted from food to
the person who eats it, are not very resistant to heat.
The
most common application is pasteurization of liquid milk. In the
case of milk, the pathogenic organism that is of classical importance
is Mycobacterium tuberculosis, and the time/temperature curve
for the inactivation of this bacillus is shown in Fig. 6.7.
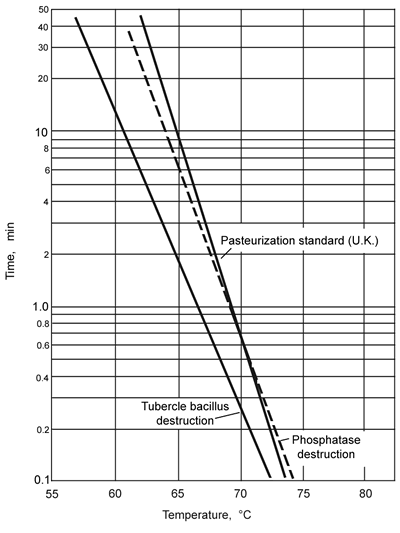
Figure 6.7 Pasteurization curves for milk
This curve can be applied to determine the necessary holding time and
temperature in the same way as with the sterilization thermal death curves.
However, the times involved are very much shorter, and controlled rapid
heating in continuous heat exchangers simplifies the calculations so that
only the holding period is really important. For example, 30 min at 62.8°C
in the older pasteurizing plants and 15 sec at 71.7°C in the so-called
high temperature/short time (HTST) process are sufficient.
An even faster process using a temperature of 126.7°C for 4 sec is
claimed to be sufficient. The most generally used equipment is the plate
heat exchanger and rates of heat transfer to accomplish this pasteurization
can be calculated by the methods explained previously.
An
enzyme present in milk, phosphatase, is destroyed under somewhat the same
time-temperature conditions as the M. tuberculosis and, since
chemical tests for the enzyme can be carried out simply, its presence
is used as an indicator of inadequate heat treatment. In this case, the
presence or absence of phosphatase is of no significance so far as the
storage properties or suitability for human consumption are concerned.
Enzymes
are of importance in deterioration processes of fruit juices, fruits and
vegetables. If time-temperature relationships, such as those that are
shown in Fig. 6.7 for phosphatase, can be determined for these enzymes,
heat processes to destroy them can be designed. Most often this is done
by steam heating, indirectly for fruit juices and directly for vegetables
when the process is known as blanching.
The
processes for sterilization and pasteurization illustrate very well the
application of heat transfer as a unit operation in food processing. The
temperatures and times required are determined and then the heat transfer
equipment is designed using the equations developed for heat-transfer
operations.
EXAMPLE
6.6. Pasteurisation of milk
A pasteurization heating process for milk was found, taking measurements
and times, to consist essentially of three heating stages being 2 min
at 64°C, 3 min at 65°C and 2 min at 66°C. Does this process
meet the standard pasteurization requirements for the milk, as indicated
in Fig. 6.7, and if not what adjustment needs to be made to the period
of holding at 66°C?
From
Fig. 6.7, pasteurization times tT can be read off
the UK pasteurisation standard, and from and these and the given times,
rates and fractional extents of pasteurization can be calculated:
At 64°C, t64
= 15.7 min
so 2 min is 2
= 0.13
15.7
At 65°C,
t65 = 9.2 min
so 3 min is 3
= 0.33
9.2
At 66°C,
t66 = 5.4 min
so 2 min is 2
= 0.37
5.4
Total pasteurization
extent = (0.13 + 0.33 + 0.37) = 0.83.
Pasteurization remaining
to be accomplished = (1 - 0.83) = 0.17.
At 66°C this would be obtained from (0.17 x 5.4) min holding = 0.92
min.
So an additional 0.92 min (or approximately 1 min) at 66°C would be
needed to meet the specification.
 Heat-Transfer
Applications > REFRIGERATION, CHILLING AND FREEZING
 Back
to the top |
Thermal
Death Time