Energy
balances can be calculated on the basis of external energy used per kilogram
of product, or raw material processed, or on dry solids. or some key component.
The energy consumed in food production includes direct energy which is
fuel and electricity used on the farm, in transport, in factories, in
storage, selling, etc.; and indirect energy which is used to build the
machines, to make the packaging, to produce the electricity and the oil
and so on. Food itself is a major energy source, and energy balances can
be determined for animal or human feeding; food energy input can be balanced
against outputs in heat and mechanical energy and chemical synthesis.
In the SI system there is only one energy unit, the joule. However, kilocalories
are still used by some nutritionists, and British thermal units (Btu)
in some heat-balance work.
The
two applications used in this book are heat balances, which are the basis
for heat transfer, and the energy balances used in analysing fluid flow.
Heat Balances
The most common important energy form is heat energy and the conservation
of this can be illustrated by considering operations such as heating and
drying. In these, enthalpy (total heat) is conserved and as with
the mass balances so enthalpy balances can be written round the various
items of equipment. or process stages, or round the whole plant, and it
is assumed that no appreciable heat is converted to other forms of energy
such as work.
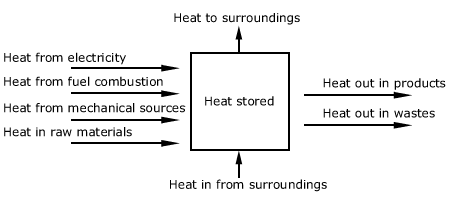
Figure 2.2. Heat balance.
Enthalpy (H) is always referred to some reference level or datum,
so that the quantities are relative to this datum.
Working out energy balances is then just a matter of considering the various
quantities of materials involved, their specific heats, and their changes
in temperature or state (as quite frequently latent heats arising from
phase changes are encountered). Fig. 2.2 illustrates the heat balance.
Heat is absorbed or evolved by some reactions
in food processing but usually the quantities are small when compared
with the other forms of energy entering into food processing such as sensible
heat and latent heat. Latent heat is the heat required to change,
at constant temperature. the physical state of materials from solid to
liquid, liquid to gas, or solid to gas. Sensible heat is that heat
which when added or subtracted from food materials changes their temperature
and thus can be sensed.
The units of specific heat (c) are J kg-1 °C-1,
and sensible heat change is calculated by multiplying the mass by the
specific heat by the change in temperature, m c DT,
(J).
The units of latent heat are J kg-1 and total latent heat change
is calculated by multiplying the mass of the material, which changes its
phase, by the latent heat. Having determined those factors that are significant
in the overall energy balance, the simplified heat balance can then be
used with confidence in industrial energy studies. Such calculations can
be quite simple and straightforward but they give a quantitative feeling
for the situation and can be of great use in design of equipment and process.
 EXAMPLE
2.10. Heat demand in freezing bread
It is desired to establish freezing of 10,000 loaves
of bread each weighing 0.75 kg from an initial room temperature of 18°C
to a final store temperature of -18°C. If this is to be carried out
in such a way that the maximum heat demand for the freezing is twice the
average demand, estimate this maximum demand, if the total freezing time
is to be 6 h.
If data on the particular bread are unavailable, in the literature are
data on bread constituents, calculation methods, enthalpy/temperature
tables
(a)
Tabulated data (Appendix 7) suggests specific
heat above freezing 2.93 kJ kg-1 °C-1, below
freezing 1.42 kJ kg-1 °C-1, latent heat of freezing
115 kJ kg-1 and freezing temperature is -2°C.
Total enthalpy
change, (DH)
= [18 - (-2)] 2.93 + 115 + [-2 - (-18)] 1.42 = 196 kJ kg-1.
(b) Formula (Appendix
7) assuming the bread is 36% water gives
- specific heat above freezing
4.2 x 0.36 + 0.84 x 0.64 = 2.05 kJ kg-1
°C-1,
- specific heat below freezing
2.1 x 0.36 + 0.84 x 0.64 = 1.29 kJ kg-1
°C-1,
- latent heat
0.36
x 335 =
121 kJ kg-1.
Total enthalpy change, (DH)
= [18 - (-2)]2.05 + 121 +[-2-(-18)] 1.29 = 183 kJ kg-1.
(c) Enthalpy/temperature
data for bread of 36% moisture (Mannheim et
al., 1957) suggest
H18.3°C = 210.36 kJ kg-1,
H-17.3°C = 65.35 kJ kg-1.
So from +18°C
to -18°C total enthalpy change (DH
) = 210 - 65 = 145 kJ kg-1.
(d) The enthalpy/temperature
data in Mannheim et al. can also be used to estimate "apparent"
specific heats as
DH
/DT
= c and so using the data:
| T°C |
= |
-20.6
|
-17.8
|
15.6
|
18.3
|
| H kJ
kg-1 |
= |
55.88
|
65.35
|
203.4
|
210.4
|
| Giving
c-18 = |
DH
|
=
|
65.35
- 55.88
|
=
3.4 kJ kg-1 °C-1
|
|
|
|
|
DT
|
20.6
- 17.8
|
| Giving
c18 = |
DH
|
=
|
210.4
- 203.4
|
=
2.6 kJ kg-1 °C-1
|
|
|
|
|
DT
|
18.3
– 15.6
|
Note that the "apparent" specific heat at -18°C, 3.4 kJ
kg-1 °C is higher than the specific heat below freezing
in (a), 1.42, and in (b) , 1.29 kJ kg-1 °C-1.
The reason for the high apparent specific heat at -18°C is due to
some freezing still continuing at this temperature. It is suggested that
at -18°C only about two-thirds of the water is actually frozen to
ice. This implies only two-thirds of the latent heat has been extracted
at this temperature. Making this adjustment to the latent-heat terms,
estimates for the total emthalph change (a) and (b) give 158kJ kg-1
and 142kJ kg-1 respectively, much improving the agreement with
(c) of 145 kJ kg-1.
Taking DH
= 150 kJ kg-1
Total
heat change
= 150 x 10,000
x 0.75 = 1.125 x 106 kJ.
Total time =
6h = 2.16 x 104s.
(DH
/Dt)
= 52 kJ s-1 = 52 kW on average.
And if the maximum
rate of heat removal is twice the average:
(DH
/Dt)
max = 2 x 52 = 104 kW.
Example 2.10 illustrates the application of heat balances, and
it also illustrates the advisability of checking or obtaining corroborative
data unless reliable experimental results are available for the particular
system that is being considered. The straightforward application of the
tabulated overall data would have produced a result about 30% higher than
that finally calculated. On the other hand, for some engineering calculations
to be within 30% may be about as close as you can get.
In
some cases, it is adequate to make approximations to heat balances by
isolating dominant terms and ignoring less important ones. To make approximations
with any confidence, it is necessary to be reasonably sure about the relative
magnitudes of the quantities involved. Having once determined the factors
that dominate the heat balance, simplified balances can then be set up
if appropriate to the circumstances and used with confidence in industrial
energy studies. This simplification reduces the calculation effort, focuses
attention on the most important terms, and helps to inculcate in the engineer
a quantitative feeling for the situation.
EXAMPLE
2.11. Dryer heat balance for casein drying
In drying casein the dryer is found to consume 4 m3/h
of natural gas with a calorific value of 800 kJ/mole. If the throughput
of the dryer is 60 kg of wet casein per hour, drying it from 55% moisture
to 10% moisture, estimate the overall thermal efficiency of the dryer
taking into account the latent heat of evaporation only.
Basis: 1 hour of operation
60 kg of wet casein
contains 60 x 0.55 kg water = 33 kg moisture
and
60 x (1 - 0.55) = 27 kg bone
dry casein.
As the final product
contains 10% moisture, the moisture in the product is 27/9 = 3 kg
and so moisture removed =
(33 - 3) = 30 kg
Latent
heat of evaporation = 2257 kJ kg-1(at 100 °C from
Appendix 8)
so heat necessary to supply = 30
x 2257 = 6.8 x l04 kJ
Assuming the natural
gas to be at standard temperature and pressure at which 1 mole occupies
22.4 litres
| |
Rate
of flow of natural gas = 4 m3 h-1 = |
4
x 1000
|
=
179 moles h-1
|
|
|
|
22.4
|
 |
Heat
available from combustion =
179 x 800 =
14.3 x 104 kJ/h |
| Approximate
thermal efficiency of dryer = |
heat
needed
|
=
6.8 x 104 / 14.3 x 104 = 48%
|
|
|
|
heat
used
|
To evaluate this efficiency
more completely it would be necessary to take into account the sensible
heat of the dry casein solids and the moisture, and the changes in temperature
and humidity of the combustion air, which would be combined with the natural
gas. However, as the latent heat of evaporation is the dominant term the
above calculation gives a quick estimate and shows how a simple energy
balance can give useful information.
Similarly energy balances can be carried out over thermal processing operations,
and indeed any processing operations in which heat or other forms of energy
are used.
EXAMPLE
2.12. Heat balance for cooling pea soup after canning
An autoclave contains 1000 cans of pea soup. It is heated to an overall
temperature of 100°C. If the cans are to be cooled to 40°C before
leaving the autoclave, how much cooling water is required if it enters
at 15°C and leaves at 35°C?
The specific heats of the pea soup and the can metal are respectively
4.1 kJ kg-1 °C-1 and 0.50 kJ kg-1°C-1.
The weight of each can is 60 g and it contains 0.45 kg of pea soup. Assume
that the heat content of the autoclave walls above 40°C is 1.6 x 104
kJ and that there is no heat loss through the walls.
Let w =
the weight of cooling water required;
and the datum temperature be 40°C, the temperature of the cans
leaving the autoclave.
Heat entering
Heat added to cans = weight of cans x specific heat x temperature above
datum
=
1000 x 0.06 x 0.50 x (100 - 40) kJ = 1.8 x 103 kJ.
Heat added to can contents = weight pea soup x specific heat x temperature
above datum
=
1000 x 0.45 x 4.1 x (100 - 40)
=
1.1 x 105 kJ.
Heat added
to water = weight of water x specific heat x temperature above datum
=
w x 4.21 x (15 - 40) (Appendix
4)
=
-104.6 w kJ.
Heat leaving
Heat in cans = 1000 x 0.06 x 0.50 x (40 - 40) (cans leave at datum temperature)
=
0.
Heat in can contents = 1000 x 0.45 x 4.1 x (40 – 40)
=
0.
Heat in water =
w x 4.186 x (35 - 40)
=
-20.9 w.
HEAT-ENERGY
BALANCE OF COOLING PROCESS; 40°C AS DATUM LINE
| Heat
entering |
(kJ)
|
|
Heat
Leaving |
(kJ) |
| Heat in cans |
1,800 |
|
Heat in cans |
0 |
| Heat in can
contents |
110,000 |
|
Heat in can
contents |
0 |
| Heat in autoclave
wall |
16,000 |
|
Heat in autoclave
wall |
0 |
| Heat in water |
105.3w
|
|
Heat in water |
-20.9 w |
| Total heat entering |
127,800 -105.3w |
|
Total heat leaving |
-20.9 w |
|
|
|
|
|
|
Total
heat entering
|
=
|
Total
heat leaving
|
|
|
127,800
- 105.3w
|
=
|
-20.9
w
|
|
| And so |
w
|
=
|
1514
kg
|
|
| Amount
of cooling water required = 1514 kg. |
|
|
|
Other Forms of Energy
The most common mechanical energy is motor power and
it is usually derived, in food factories, from electrical
energy but it can be produced from steam engines or water power. The electrical
energy input can be measured by a suitable wattmeter, and the power used
in the drive estimated. There are always losses from the motors due to
heating, friction and windage; the motor efficiency, which can normally
be obtained from the motor manufacturer, expresses the proportion (usually
as a percentage) of the electrical input energy which emerges usefully
at the motor shaft and so is available.
When
considering movement, whether of fluids in pumping, of solids in solids
handling, or of foodstuffs in mixers, the energy input is largely mechanical.
The flow situations can be analysed by recognising the conservation of
total energy whether as energy of motion, or potential energy such as
pressure energy, or energy lost in friction. Similarly, chemical energy
released in combustion can be calculated from the heats of combustion
of the fuels and their rates of consumption. Eventually energy emerges
in the form of heat and its quantity can be estimated by summing the various
sources.
EXAMPLE
2.13. Refrigeration load in bread freezing
The bread-freezing operation of Example 2.10 is to be carried out
in an air-blast freezing tunnel. It is found that the fan motors are rated
at a total of 80 horsepower and measurements suggest that they are operating
at around 90% of their rating, under which conditions their manufacturer's
data claims a motor efficiency of 86%.
If 1 ton of refrigeration is 3.52 kW, estimate the maximum refrigeration
load imposed by this freezing installation assuming (a) that fans and
motors are all within the freezing tunnel insulation and (b) the fans
but not their motors are in the tunnel. The heat-loss rate from the tunnel
to the ambient air has been found to be 6.3 kW.
Extraction rate
from freezing bread (maximum) = 104 kW
Fan rated horsepower = 80
Now 0.746 kW = 1
horsepower (Appendix 2) and the motor is operating
at 90% of rating,
and so (fan + motor) power = (80 x 0.9) x 0.746
=
53.7 kW
(a) With motors
+ fans in tunnel
heat load from
fans + motors = 53.7 kW
heat load from ambient
= 6.3 kW
Total heat load =
(104 + 53.7 + 6.3) kW
=
164 kW
=
164/3.52 = 46 tons of refrigeration
(see Appendix 2)
(b) With motors
outside, the motor inefficiency = (1 - 0.86) does not impose a load on
the refrigeration.
Total heat load
=
(104 + [0.86 x 53.7] + 6.3)
=
156kW
=
156/3.52 = 44.5 tons refrigeration
In practice, material and energy balances are often combined as the same
stoichiometric information is needed for both.
 Material
& Energy Balances > SUMMARY & PROBLEMS
 Back
to the top |
Heat
balances
enthalpy