When
the mixture has been thoroughly dispersed, it is assumed that the
components are distributed through the volume in accordance with their
overall proportions. The probability that any particle picked at random
will be component Q will be q, and (1 - q) that it
is not Q. Extending this to samples containing N particles, it
can be shown, using probability theory, that:
sr2
= p(1 - p)/N = so2/N.
(12.3)
This
assumes that all the particles are equally sized and that each particle
is either pure P or pure Q. For example, this might be the
mixing of equal-sized particles of sugar and milk powder. The subscripts
o and r have been used to denote the initial and the random values
of s2, and inspection of the formulae, eqn. (12.2) and
eqn. (12.3), shows that in the mixing process the value of s2
has decreased from p(1 - p) to 1/Nth of this value. It has
been suggested that intermediate values between so2
and sr2 could be used to show the progress
of mixing. Suggestions have been made for a mixing index, based
on this, for example:
(M) = (so2
- s2)/(so2 - sr2)
(12.4)
which is so designed
that (M) goes from 0 to 1 during the course of the mixing process.
This measure can be used for mixtures of particles and also for the mixing
of heavy pastes.
 EXAMPLE
12.2. Mixing of yeast into dough
For a particular bakery operation, it was desired to mix dough in 95 kg
batches and then at a later time to blend in 5 kg of yeast. For product
uniformity it is important that the yeast be well distributed and so an
experiment was set up to follow the course of the mixing. It was desired
to calculate the mixing index after 5 and 10 min mixing.
Sample yeast compositions, expressed as the percentage of yeast in 100
g samples were found to be:
After 5 min
(%) 0.0
16.5 3.2 2.2 12.6 9.6 0.2 4.6
0.5 8.5
Fractional 0.0 0.165 0.032.......
After 10 min
(%) 3.4
8.3 7.2 6.0 4.3 5.2
6.7 2.6 4.3 2.0
Fractional 0.034 0.083 ..........
Using the formula 1/n[S(x1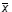2)]
- ( )2
Calculating
s52 = 3.0 x 10-3
s102 = 3.8 x 10-4
The value of so2 = 0.05 x 0.95 = 4.8
x 10-2
and sr2
»
0 as the number of "particles" in a sample is very large,
(M)5 = (4.8 - 0.3)/(4.8 - 0)
= 0.93
(M)10 =
(4.8 - 0.04)/4.8 - 0)
= 0.99.
Mixing of Widely Different Quantities
The mixing of particles varying substantially in size or in density presents
special problems, as there will be gravitational forces acting in the
mixer which will tend to segregate the particles into size and density
ranges. In such a case, initial mixing in a mixer may then be followed
by a measure of (slow gravitational) un-mixing and so the time of mixing
may be quite critical.
Mixing
is simplest when the quantities that are to be mixed are roughly in the
same proportions. In cases where very small quantities of one component
have to be blended uniformly into much larger quantities of other components,
the mixing is best split into stages, keeping the proportions not
too far different in each stage. For example, if it were required to add
a component such that its final proportions in relatively small fractions
of the product are 50 parts per million, it would be almost hopeless to
attempt to mix this in a single stage. A possible method might be to use
four mixing stages, starting with the added component in the first of
these at about 30:1. In planning the mixing process it would be wise to
take analyses through each stage of mixing, but once mixing times had
been established it should only be necessary to make check analyses on
the final product.
EXAMPLE
12.3. Mixing vitamin addition into powdered cereal
It is desired to mix vitamin powder at the level of 10-3 %
by weight into a 1 tonne batch of powdered cereal. Two double-cone blenders
are available, one (L) with a capacity of 100 to 500 kg powder and another
(S) with a capacity of 1 to 10 kg. Both will mix adequately in 10 min
so long as the minor constituent constitutes not less than 10%. Suggest
a procedure for the mixing.
Total weight vitamin
needed = 1000 x 10-5 kg = 10 g
Divide into two, 2 x 5 g as two final 500 kg batches will be needed. Then:
1. Hand blend 5
g and 50 g cereal ®
mixture (1), and then (1) and 945 g cereal ®
mixture (2). This
may need analytical checking to set up a suitable hand-mixing procedure.
2. Take (2) + 9 kg cereal and mix in mixer (S) ®
mixture (3).
3. Take (3) + 90 kg cereal and mix in (L) ®
mixture (4).
4. Take (4) + 400kg cereal and mix in (L) ®
mixture (5) - product.
5. Repeat, with other 5 g vitamin and 500 kg cereal, steps (1) to (4).
Rates of Mixing
Once a suitable measure of mixing has been found, it becomes possible
to discuss rates of accomplishing mixing. It has been assumed that the
mixing index ought to be such that the rate of mixing at any time, under
constant working conditions such as in a well-designed mixer working at
constant speed, ought to be proportional to the extent of mixing remaining
to be done at that time. That is,
dM/dt = K[(1 - (M))]
(12.5)
where
(M) is the mixing index and K is a constant, and on integrating
from t = 0 to t = t during which (M) goes from 0
to (M),
[(1
- (M))] = e-Kt
or (M) = 1 - e-Kt
(12.6)
This
exponential relationship, using (M) as the mixing index, has been
found to apply in many experimental investigations at least over two or
three orders of magnitude of (M). In such cases, the constant K
can be related to the mixing machine and to the conditions and it can
be used to predict, for example, the times required to attain a given
degree of mixing.
EXAMPLE
12.4. Blending starch and dried vegetables for a soup mix
In a batch mixer, blending starch and dried-powdered vegetables for a
soup mixture, the initial proportions of dried vegetable to starch were
40:60. If the variance of the sample compositions measured in terms of
fractional compositions of starch was found to be 0.0823 after 300 s of
mixing, for how much longer should the mixing continue to reach the specified
maximum sample composition variance for a 24 particle sample of 0.02?
Assume
that the starch and the vegetable particles are of approximately the same
physical size.
Then taking the fractional
content of dried vegetables to be p = 0.4,
(1 - p) = (1 - 0.4) = 0.6
so2 = 0.4 x 0.6 = 0.24
sr2 = s02/N =
0.24/24 from eqn. (12.3)
= 0.01
Substituting in eqn. (12.4) we have:
(M) = (so2 - s2)/(so2
- sr2)
= (0.24 - 0.0823)/(0.24 - 0.01)
= 0.685
Substituting in eqn.12.6
e-300K = 1 - 0.685 = 0.315
300K = 1.155,
K = 3.85 x 10-3
For s2
= 0.02,
(M) = (0.24 - 0.02)/(0.24 - 0.01)
= 0.957
0.957 = 1 - e-0.00385t
- 0.043 = - e-0.00385t
3.147 =
0.00385t
t = 817s, say 820 s,
the additional
mixing time would be 820s - 300 s = 520 s.
Energy Input in Mixing
Quite substantial quantities of energy can be consumed in some types of
mixing, such as in the mixing of plastic solids. There is no necessary
connection between energy consumed and the progress of mixing: to take
an extreme example there could be shearing along one plane in a sticky
material, then recombining to restore the original arrangement, then repeating
which would consume energy but accomplish no mixing at all. However, in
well-designed mixers energy input does relate to mixing progress, though
the actual relationship has normally to be determined experimentally.
In the mixing of flour doughs using high-speed mixers, the energy consumed,
or the power input at any particular time, can be used to determine the
necessary mixing time. This is a combination of mixing with chemical reaction
as flour components oxidize during mixing in air which leads to increasing
resistance to shearing and so to increased power being required to operate
the mixer.
EXAMPLE
12.5. Mixing time for bread dough
In a particular mixer used for mixing flour dough for breadmaking, it
has been found that mixing can be characterized by the total energy consumed
in the mixing process and that sufficient mixing has been accomplished
when 8 watt hours of energy have been consumed by each kg of dough.
Such a mixer, handling 2000 kg of dough, is observed just after starting
to be consuming 80 amperes per phase, which rises steadily over 10s to
400 amperes at which level it then remains effectively constant. The mixer
is driven by a 440-volt, 3-phase electric motor with a power factor (cos
f))
of 0.89, and the overall mechanical efficiency between motor and mixing
blades is 75%. Estimate the necessary mixing time.
Power
to the motor = Ö3
EI cosf
where I is the current per phase and E and cosf
in this case are 440 volts and 0.89, respectively.
In first 10 s, Iaverage = ½(80 + 400) = 240
amperes.
Energy consumed
in first 10 s
= power x time = Ö3
EI cosf
= Ö3
x 440
x 0.75 x 240 x 0.89 x 10/3600
= 339 watt h
= 339/2000
= 0.17 W h kg-1.
Energy still needed
after first 10 s
= (8 - 0.17)
= 7.83 W h kg-1.
Additional time needed,
at steady 400 ampere current
= (7.83 x 2000 x 3600)/(1.73 x 440 x 0.75 x 400 x 0.89)
= 277 s.
Total time = 277 + 10 s = 4.8
min.
In
actual mixing of doughs the power consumed would decrease slowly and more
or less uniformly, but only by around 10-15% over the mixing process.
 Mixing
> LIQUID MIXING
 Back
to the top |
Mixing
of Widely Different Quantities