Unit Operations in Food Processing

As evaporation proceeds, the liquor remaining in the evaporator becomes more concentrated and its boiling point will rise. The extent of the boiling-point elevation depends upon the nature of the material being evaporated and upon the concentration changes that are produced. The extent of the rise can be predicted by Raoult's Law, which leads to:

DT = kx (8.3)

where DT is the boiling point elevation, x is the mole fraction of the solute and k is a constant of proportionality.

In multiple effect evaporators, where the effects are fed in series, the boiling points will rise from one effect to the next as the concentrations rise. Relatively less of the apparent temperature drops are available for heat transfer, although boiling points are higher, as the condensing temperature of the vapour in the steam chest of the next effect is still that of the pure vapour. Boiling-point elevation complicates evaporator analysis but heat balances can still be drawn up along the lines indicated previously. Often foodstuffs are made up from large molecules in solution, in which boiling-point elevation can to a greater extent be ignored.

As the concentrations rise, the viscosity of the liquor also rises. The increase in the viscosity of the liquor affects the heat transfer and it often imposes a limit on the extent of evaporation that is practicable.

There is no straightforward method of predicting the extent of the boiling-point elevation in the concentrated solutions that are met in some evaporators in practical situations. Many solutions have their boiling points at some concentrations tabulated in the literature, and these can be extended by the use of a relationship known as Duhring's rule. Duhring's rule states that the ratio of the temperatures at which two solutions (one of which can be pure water) exert the same vapour pressure is constant.
Thus, if we take the vapour pressure/temperature relation of a reference liquid, usually water and if we know two points on the vapour pressure-temperature curve of the solution that is being evaporated, the boiling points of the solution to be evaporated at various pressures can be read off from the diagram called a Duhring plot. The Duhring plot will give the boiling point of solutions of various concentrations by interpolation, and at various pressures by proceeding along a line of constant composition. A Duhring plot of the boiling points of sodium chloride solutions is given in Fig. 8.3.

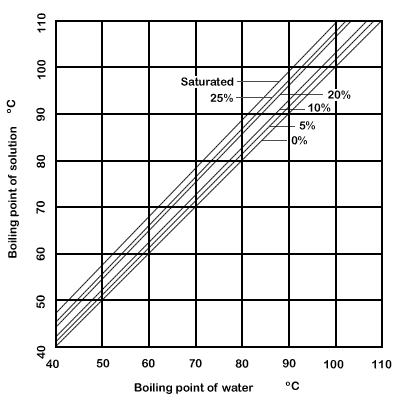
FIG. 8.3 Duhring plot for boiling point of sodium chloride solutions
Figure 8.3 Duhring plot for boiling point of sodium chloride solutions

EXAMPLE 8.5. Duhring Plot for sodium chloride solutions
It is found that a saturated solution of sodium chloride in water boils under atmospheric pressure at 109°C. Under an absolute pressure of 25.4 kPa, water boils at 65.6°C and saturated sodium chloride at 73.3°C. From these, draw a Duhring plot for saturated salt solution. Knowing the vapour pressure/temperature relationship for water from Fig. 7.2, find the boiling temperature of saturated salt solution under a total pressure of 33.3kPa.

The Duhring plot for salt solution has been given in Fig. 8.3, and since the line is straight, it may be seen that knowledge of two points on it, and the corresponding boiling points for the reference substance, water, would enable the line to be drawn.

From the line, and using Fig. 7.2 again, it is found that:
the boiling point of water under a pressure of 33.3 kPa is 71.7°C,
we can read off the corresponding boiling temperature for saturated salt solution as 79.4°C.

By finding the boiling points of salt solutions of various concentrations under two pressures, the Duhring lines can then, also, be filled in for solutions of these concentrations. Such lines are also on Fig.8.3. Intermediate concentrations can be estimated by interpolation and so the complete range of boiling points at any desired concentration, and under any given pressure, can be determined.

Latent heats of vaporization also increase as pressures are reduced, as shown for water in Table 7.1. Methods for determining these changes can be found in the literature, for example in Perry (1997).

Evaporation > EVAPORATION OF HEAT-SENSITIVE MATERIALS

Back to the top